Calculus II 08.01 Basic Integration Rules

Previous	Calculus II 07 Integration Applications
Next	Calculus II 08.02 Integration by Parts

8.1 Basic Integration Rules

• Review procedures for fitting an integrand to one of the basic integration rules.

Fitting Integrands to Basic Integration Rules

A major step in solving any integration problem is recognizing which basic integration rule to use. See Integration Rules

Example 8.1.1 Comparing Three Similar Integrals

Find each integral.

$$\textbf{a. } \int \frac{4}{x^{2}+9}dx $$

$$\textbf{b. } \int \frac{4x}{x^{2}+9}dx $$

$$\textbf{c. } \int \frac{4x^{2}}{x^{2}+9}dx $$

Solution
a. Use the Arctangent Rule and let \(u=x\) and \(a=3\).

$$ \int \frac{4}{x^{2}+9}dx $$	$$ = 4 \int \frac{1}{x^{2}+3^{2}}dx $$	Constant Multiple Rule
	$$ = 4 \left( \frac{1}{3} \arctan \frac{x}{3} \right) + C \:\:\:\: $$	Arctangent Rule
	$$ = \frac{4}{3} \arctan \frac{x}{3} + C $$	Simplify.

b. The Arctangent Rule does not apply because the numerator contains the variable \(x\). Consider the Log Rule and let \(u=x^{2}+9\). Then \(du=2x\:dx\), producing

$$ \int \frac{4x}{x^{2}+9}dx $$	$$ = 2 \int \frac{2x}{x^{2}+9}dx $$	Constant Multiple Rule
	$$ = 2 \int \frac{du}{u} $$	Substitution: \(u=x^{2}+9\)
	$$ = 2\: \ln \left |u \right | + C $$	Log Rule
	$$ = 2\:\ln(x^{2}+9) + C \:\:\:\: $$	Substitution: \(u=x^{2}+9\)

c. Because the numerator's degree equals the denominator's, you should first use long division to rewrite the improper rational function as a polynomial plus a proper rational function.

$$\int \frac{4x^{2}}{x^{2}+9}dx $$	$$ = \int \left( 4 + \frac{-36}{x^{2}+9} \right) dx $$	Rewrite using long division
	$$ = \int 4\:dx - 36 \int \frac{1}{x^{2}+9}\:dx $$	Write as two integrals.
	$$ = 4x - 36 \left( \frac{1}{3} \arctan \frac{x}{3} \right) + C \:\:\:\: $$	Integrate using the Arctangent Rule
	$$ = 4x - 12 \arctan \frac{x}{3} + C $$	Simplify.

Example 8.1.2 Solving a Single Integral using Two Basic Rules

The region's area is \(\approx\) 1.839. Figure 8.1.1

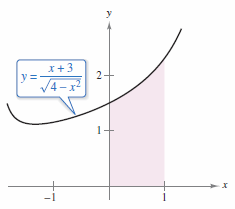
Evaluate $$ \int_{0}^{1} \frac{x+3}{ \sqrt{4-x^{2}}}dx .$$ Solution Simplify the integral by breaking it in two. Then apply the Power and Arcsine Rules. See Figure 8.1.1 $$ \int_{0}^{1} \frac{x+3}{ \sqrt{4-x^{2}}}dx $$ $$ = \int_{0}^{1} \frac{x}{ \sqrt{4-x^{2}}}dx + \int_{0}^{1} \frac{3}{ \sqrt{4-x^{2}}}dx $$ Separate the integral. $$ = -\frac{1}{2} \int_{0}^{1} (4-x^{2})^{-\frac{1}{2}}(-2x) dx + 3 \int_{0}^{1} \frac{1}{\sqrt{2^{2}-x^{2}}}dx \:\:\:\:$$ Apply the Power Rule. $$ = \left[ -(4-x^{2})^{\frac{1}{2}} + 3 \arcsin \frac{x}{2} \right]_{0}^{1} $$ Apply the Arcsine Rule. $$ = \left( -\sqrt{3} + \frac{\pi}{2} \right) - (-2+0) \approx 1.839$$ Simplify

Example 8.1.3 A Substitution using \(a^{2}-u^{2}\)

Some integration rules have expressions with the sum or difference between two squares, \(a^{2}-u^{2}\), \(a^{2}+u^{2}\), and \(u^{2}-a^{2}\).
Find

$$ \int \frac{x^{2}}{\sqrt{16-x^{6}}}dx .$$

Solution Because the radical in the denominator can be written in the form

$$ \sqrt{ a^{2}-u^{2} } = \sqrt{4^{2}-(x^{3})^{2}} $$

the substitution \(u=x^{3}\) gives \(du=3x^{2}dx\), and produces the following solution

$$\int \frac{x^{2}}{\sqrt{16-x^{6}}}dx $$	$$ = \frac{1}{3} \int \frac{3x^{2}}{\sqrt{16-(x^{3})^{2}}}dx \:\:\:\: $$	Rewrite the integral.
	$$= \frac{1}{3} \int \frac{du}{\sqrt{4^{2}-u^{2}}} $$	Substitution: \(u=x^{3}\)
	$$= \frac{1}{3} \arcsin \frac{u}{4} + C $$	Arcsine Rule
	$$= \frac{1}{3} \arcsin \frac{x^{3}}{4} + C $$	Substitution: \(x^{3}=u\)

Example 8.1.4 The Log Rule in Disguise

Find how to use the Log Rule to evaluate

$$ \int \frac{1}{1+e^{x}}dx .$$

Solution The integral does not appear to fit any rule. The quotient form does suggest the Log Rule. If \(u=1+e^{x}\), then \(du=e^{x}\). Adding and subtracting \(e^{x}\) in the numerator produces the required \(du\).

$$ \int \frac{1}{1+e^{x}}dx $$	$$ = \int \frac{1+e^{x}-e^{x}}{1+e^{x}}dx $$	Add and subtract \(e^{x}\) in the numerator.
	$$= \int \left( \frac{1+e^{x}}{1+e^{x}}-\frac{e^{x}}{1+e^{x}} \right)\:dx \:\:\:\:$$	Rewrite as two fractions.
	$$= \int dx- \int \frac{e^{x}dx}{1+e^{x}} $$	Rewrite as two integrals.
	\(= x-\ln \left( 1+e^{x} \right) + C \)	Integrate.

Example 8.1.5 The Power Rule in Disguise

Find

$$ \int (\cot x) \left[ \ln(\sin x) \right]\: dx .$$

Solution Consider the two primary choices for \(u\)

$$ u=\cot x \text{ or }u=\ln(\sin x) $$

and choose the one that makes the integral easier to solve. The second choice uses the Power Rule. Applying that

$$u=\ln(\sin x) \text{ and }du=\frac{\cos x}{\sin x}dx=\cot x\:dx $$

This produces

$$ \int (\cot x) [\ln(\sin x)]dx $$	$$ = \int u\:du $$	Substitution: \(u=\ln(\sin x)\)
	$$ = \frac{u^{2}}{2}+C $$	Integrate
	$$= \frac{1}{2} \left[\ln(\sin x) \right]^{2}+C \:\:\:\:$$	Rewrite in \(x\) terms.

Example 8.1.6 Using Trigonometric Identities

Find

$$ \int \tan^{2}2x\:dx .$$

Solution Note that \(\tan^{2}u\) does not fit a basic integration rule. But \(\sec^{2}u\) is. Using the trigonometric identity \(\tan^{2}u=\sec^{2}-1\) lets \(u=2x\) and \(du=2\:dx\). This produces

$$ \int \tan^{2}2x\:dx $$	$$= \frac{1}{2} \int \tan^{2}u\:du $$	Substitution: \(u=2x\)
	$$= \frac{1}{2} \int ( \sec^{2}-1)\:du $$	Trigonometric identity
	$$= \frac{1}{2} \int \sec^{2}u\:du - \frac{1}{2} \int \:du \:\:\:\:$$	Rewrite as two integrals
	$$= \frac{1}{2} \tan u - \frac{u}{2} + C $$	Integrate
	$$= \frac{1}{2} \tan 2x - x + C $$	Substitute: \(2x=u\)

Internal Links

Parent Article: Calculus II 08 Integration Techniques