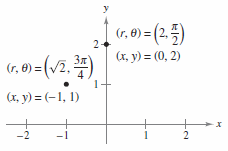Calculus II 10.04 Polar Coordinates and Polar Graphs
| Previous | Calculus II 10.03 Parametric Equations and Calculus |
| Next | Calculus II 10.05 Area and Arc Length in Polar Coordinates |
Contents
10.4 Polar Coordinates and Polar Graphs
- Understand the polar coordinate system.
- Translate cartesian coordinates and equations to polar form and vice versa.
- Sketch a graph in polar form.
- Find the slope for a tangent line to a polar graph.
- Special polar graphs.
Polar Coordinates
|
|
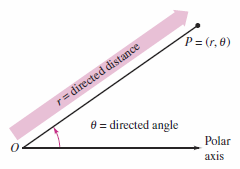
To form the polar coordinate system on the plane, fix a point \(O\), called the pole, or origin, and construct from \(O\) an initial ray called the polar axis, as shown in Figure 10.4.1. Then each point \(P\) on the plane can be assigned polar coordinates \((r,\theta)\), as follows.
Figure 10.4.2 shows three points on the polar coordinate system. Notice points are located with respect to concentric circles intersected by radial lines through the pole. In cartesian coordinates each point has a unique representation. This is not true with polar coordinates. For instance, the coordinates
represent the same point, as shown in Figure 10.4.2(b) and (c). Because \(r\) is a directed distance, the coordinates
represent the same point. In general, the point \((r,\theta)\) can be written as
or
where \(n\) is any integer. Moreover, the pole is represented by \((0,\theta)\), where \(\theta\) is any angle. |
Coordinate Conversion
|
|
To establish the relationship between polar and cartesian coordinates, let the polar axis coincide with the positive \(x\)-axis and the pole with the origin, as shown in Figure 10.4.3. Because \((x,y)\) lies on a circle with radius \(r\), it follows that
The trigonometric definitions translate to
|
Theorem 10.4.1 Polar Coordinate Conversion
The polar coordinates \((r,\theta)\) for a point are related to the cartesian coordinates \((x,y)\) for a point as follows.
| Polar-to-Cartesian | Cartesian-to-Polar |
| \(x= r \cos \theta\) | $$\tan \theta = \frac{y}{x}$$ |
| \(y= r \sin \theta\) | \(r^{2}=x^{2}+y^{2}\) |
Example 10.4.1 Polar-to-Cartesian Conversion
|
|
a. For the point \((r,\theta)=(2,\pi)\),
The cartesian coordinates are \((x,y)=(-2,0)\).
The cartesian coordinates are \((x,y)=(3/2,\sqrt{3}/2)\), as shown in Figure 10.4.4. |
Example 10.4.2 Cartesian-to-Polar Conversion
|
|
a. For the second-quadrant point \((x,y)=(-1,1)\),
Because \(\theta\) is in the same quadrant as \((x,y)\), choose a positive value for \(r\).
This proves that one polar coordinate is \((r,\theta)=(\sqrt{2},3\pi/4)\). |
Polar Graphs
|
|
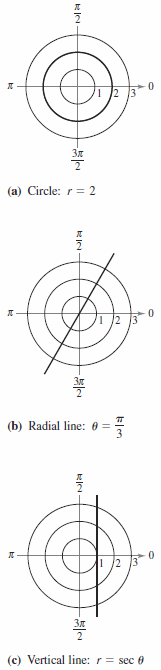
One way to sketch the graph for a polar equation is to convert to cartesian coordinates and then sketch the graph for the cartesian equation. Example 10.4.3 Graphing Polar EquationsDescribe the graph for each polar equation. Confirm each description by converting to a cartesian equation.
Solution
b. The graph for the polar equation \(\theta= \pi/3\) covers all points on the line for the angle \(\pi/3\) with the positive \(x\)-axis, as shown in Figure 10.4.6(b). This can be confirmed by using the tangent relationship, \(\tan \theta = y/x\) to obtain the regular equation
c. The graph for the polar equation \(r=\sec \theta\) is not evident by simple inspection. Begin by converting to cartesian form using the relationship \(x= r \cos \theta\).
From the cartesian equation, the graph is a vertical line, as shown in Figure 10.4.6(c). |
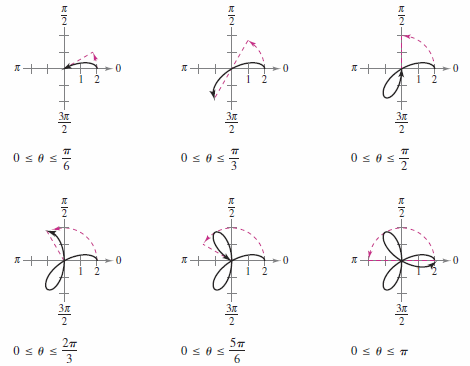
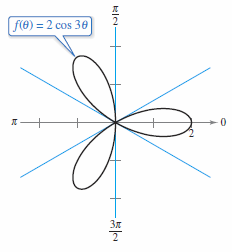
Example 10.4.4 Sketching a Polar Graph
Sketch the graph for \(r=2 \cos 3 \theta\)
Solution Begin by writing the polar equation in parametric form
- \(x= 2 \cos 3\theta \cos \theta \text{ and } y= 2 \cos 3 \theta \sin \theta \)
The entire curve, called a rose curve[1], can be sketched by letting \(\theta\) increase from 0 to \(\pi\), as shown in Figure 10.4.7. If \(\theta\) further increases from \(\pi\) to \(2\pi\) the entire curve is actually traced twice.
Note that rose curves have the form
- \(r=a \cos n \theta \text{ or } r= a \sin n \theta\)
as shown in Figure 10.4.8
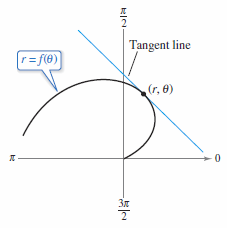
Slope and Tangent Lines
To find the slope for a tangent line to a polar graph, let \(r=f(\theta)\) be a differentiable function. To find the slope in polar form, use the parametric equations
- \(x= r \cos \theta = f(\theta) \cos \theta \text{ and } y= r \sin \theta = f(\theta) \sin \theta\).
Using the parametric form for \(dy/dx\) from Theorem 10.3.1 produces
- $$ \frac{dy}{dx} = \frac{dy/d\theta}{dx/d\theta} = \frac{ f(\theta) \cos \theta + f{}^{\prime}(\theta) \sin \theta}{-f(\theta) \sin \theta + f{}^{\prime}(\theta) \cos \theta} $$
which establishes Theorem 10.4.2.
Theorem 10.4.2 Slope in Polar Form
|
|
If \(f\) is a differentiable function for \(\theta\), then the slope for the tangent line to the graph for \(r=f(\theta)\) at the point \((r,\theta)\) is
provided that \(dx/d\theta \ne 0\) at \((r,\theta)\), as shown in Figure 10.4.9.
If \(dy/d\theta=0\) and \(dx/d\theta=0\) simultaneously, then no conclusion can be drawn about tangent lines. |
Example 10.4.5 Finding Horizontal and Vertical Tangent Lines on a Circle
|
|
Find the horizontal and vertical tangent lines for \(r= \sin \theta\), \(0\leqslant \theta \leqslant \pi\).
and
Then differentiate \(x\) and \(y\) with respect to \(\theta\) and set each derivative equal to 0.
The graph has vertical tangent lines at
and it has horizontal tangent lines at
as shown in Figure 10.4.10. |
Example 10.4.6 Finding Horizontal and Vertical Tangent Lines on a Cardioid[2]
|
|
Find the horizontal and vertical tangent lines for \(r=2(1-\cos \theta)\).
Setting \(dy/d\theta\) equal to 0 yields \(\cos \theta = -1/2\) and \(\cos \theta = 1\). Therefore, \(dy/d\theta=0\) when \(\theta=2\pi/3, \: 4\pi/3\), and 0. Let \(x= r \cos \theta\) and then differentiate with respect to \(\theta\) produces.
Setting \(dx/d\theta\) equal to 0 yields \(\sin \theta = 0\) and \(\cos \theta = 1/2\). Therefore, \(dx/d\theta=0\) when \(\theta=0, \:\pi,\: \pi/3\), and \(5\pi/3\). The graph has horizontal tangents at \((3,2\pi/3)\) and \((3,4\pi/3)\) and vertical tangents at \((1,\pi/3)\), \((1,5\pi/3)\) and \((4,\pi)\) as shown in Figure 10.4.11. Note that both derivatives are 0 when \(\theta = 0\). This information alone is insufficient to determine a horizontal or vertical tangent line at the pole. Figure 10.4.11 shows a cusp at the pole. |
Theorem 10.4.3 Tangent Lines at the Pole
|
|
Theorem 10.4.2 has an important consequence. If the graph for \(r=f(\theta)\) passes through the pole when \(\theta = \alpha\) and \(f{}^{\prime}(\alpha) \ne 0\), then the formula for \(dy/dx\) simplifies to:
The line \(\theta = \alpha \) is tangent to the graph at the pole, \((0,\alpha)\). Because a polar curve can cross the pole more than once, it can have more than one tangent line at the pole. In Figure 10.4.11, the rose curve, \(f(\theta)=2\cos 3\theta\) has three tangent lines at the pole. For this curve, \(f(\theta)=2\cos 3\theta\) is 0 when \(\theta\) is \(\pi/6\), and \(5\pi/6\). The derivative \( f{}^{\prime}(\theta)= -6 \sin 3 \theta\) is not 0 at these values for \(\theta\). |
Special Polar Graphs
Several important graph types have equations that are simpler in polar form than in cartesian form. For example, the polar equation for a circle with radius \(\alpha\) and centered at the origin is simply \(r=\alpha\). Three graph type, Limaçons, Rose Curves, and Circles are described in Figure 10.4.13. For now, several other types of graphs that have simpler equations in polar form are shown below.
Internal Links
Parent Article: Calculus II 10 Conics Parametric Equations and Polar Coordinates