Calculus III 13.07 Tangent Planes and Normal Lines

Previous	Calculus III 13.06 Directional Derivatives and Gradients
Next	Calculus III 13.08 Extrema for Functions with Two Variables

13.07 Tangent Planes and Normal Lines

• Find equations for tangent planes and normal lines to surfaces.
• Find a plane in three-dimensions, find the inclination angle.
• Compare the gradients \(\nabla f(x,y)\) and \( \nabla F(x,y,z)\).

Tangent Plane and Normal Line to a Surface

Thus far in the discussion surfaces in three-dimensions were described by equations with the form

\( z=f(x,y). \:\:\:\:\)Equation for a surface \(S\)

From now on a more general description \(F(x,y,z)=0\) will be used. For a surface \(S\) given by \(z=f(x,y)\) can be converted to the general form by defining \(F\) as

\(F(x,y,z) = f(x,y)-z\).

Because \(f(x,y)-z = 0\), consider \(S\) as the level surface for \(F\) given by

\(F(x,y,z)=0 \:\:\:\: \)Alternative equation for a surface \(S\)

Example 13.7.1 Writing an Equation for a Surface

For the function

\(F(x,y,z) = x^{2}+y^{2}+z^{2}-4\)

describe the level surface given by

\(F(x,y,z) = 0. \)

Solution The level surface given by \(F(x,y,z) = 0 \) can be written as

\( x^{2}+y^{2}+z^{2} =4\)

which is a sphere with radius 2 and centered at the origin.

Figure 13.7.1 Figure 13.7.2 Tangent plane to surface \(S\) at \(P\) Figure 13.7.3

Normal lines are useful in applications involving curves. Normal lines are equally important in analyzing surfaces and solids. For example, consider a collision between two billiard balls. When a stationary ball is struck at a point \(P\) on its surface, it moves along the impact line determined by \(P\) and the ball's center. The impact can occur in two ways. When the cue ball is moving along the impact line, it stops dead and imparts all its momentum to the stationary ball, as shown in Figure 13.7.1. When the cue ball is not moving along the impact line, it is deflected to one side or the other and retains some momentum. The momentum that is transferred to the stationary ball occurs along the impact line, no matter what direction the cue ball takes, as shown in Figure 13.7.2. This impact line is called the normal line to the surface of the ball at the point \(P\). The process for finding a normal line to a surface also produces the tangent plane to the surface. Let \(S\) be a surface given by \(F(x,y,z) = 0 \) and let \(P(x_{0},y_{0},z_{0}) \) be a point on \(S\). Let \(C\) be a curve on \(S\) through \(P\) that is defined by the vector-valued function \( \textbf{r}(t) = x(t)\textbf{i} + y(t)\textbf{j} + z(t)\textbf{k} .\) Then, for all \(t\), \(F(x(t), y(t), z(t)) = 0.\) If \(F\) is differentiable and \(x^{\prime}(t)\), \(y^{\prime}(t)\), and \(z^{\prime}(t)\) all exist, then if follows from the Chain Rule that \(0\) \(=F^{\prime}(t) \) \(= F_{x}(x,y,z)x^{\prime}(t) + F_{y}(x,y,z)y^{\prime}(t) + F_{z}(x,y,z)z^{\prime}(t).\) At \((x_{0},y_{0},z_{0})\), the equivalent vector form is $$ 0 = \color{red}{\underbrace{\color{black}{\nabla F(x_{0},y_{0},z_{0})}}_{\color{red}{\text{Gradient}}}} \cdot \color{red}{\underbrace{\color{black}{\textbf{r}^{\prime}(t_{0})}}_{\color{red}{\text{Tangent}\\ \text{vector}}}} $$ This result mean the gradient at \(P\) is orthogonal to the tangent vector for every curve on \(S\) through \(P\). Therefore, all tangent line on \(S\) lie in a plane that is normal to \( \nabla F(x_{0},y_{0},z_{0}) \) and contains \(P\), as shown in Figure 13.7.3

Definition 13.7.1 Tangent Plane and Normal Line

Let \(F\) be differentiable at the point \(P(x_{0},y_{0},z_{0})\) on the surface \(S\) given by \(F(x,y,z) = 0 \) such that

\( \nabla F(x_{0},y_{0},z_{0}) \ne \textbf{0}. \)

1. The plane through \(P\) that is normal to \( \nabla F(x_{0},y_{0},z_{0}) \) is called the tangent plane to \(S\) at \(P\).
2. The plane through \(P\) having the direction for \( \nabla F(x_{0},y_{0},z_{0}) \) is called the normal line to \(S\) at \(P\).
To find an equation for th tangent plane to \(S\) at \((x_{0},y_{0},z_{0}) \), let \((x,y,z)\) be an arbitrary point in the tangent plane. Then the vector

\(\textbf{v} = (x-x_{0})\textbf{i} + (y-y_{0})\textbf{j} + (z-z_{0})\textbf{k} \)

lies in the tangent plane. Because \( \nabla F(x_{0},y_{0},z_{0}) \) is normal to the tangent plane at \((x,y,z)\), it must be orthogonal to every vector in the tangent plane. Therefore,

\( \nabla F(x_{0},y_{0},z_{0}) \cdot \textbf{v} = 0 \)

which leads to Theorem 13.7.1.

Theorem 13.7.1 Equation for a Tangent Plane

If \(F\) is differentiable at \((x_{0},y_{0},z_{0})\), then an equation for the tangent plane to the surface \(F(x,y,z) = 0 \) at \((x_{0},y_{0},z_{0}) \) is

\( F_{x}(x_{0},y_{0},z_{0})(x-x_{0}) + F_{y}(x_{0},y_{0},z_{0})(y-y_{0}) + F_{z}(x_{0},y_{0},z_{0})(z-z_{0}) = 0.\)

To find an equation for the tangent plane at a point on a surface given by \(z=f(x,y)\), define \(F\) as

\(F(x,y,z) = f(x,y)-z\).

Then \(S\) is given by the level surface \(F(x,y,x) = 0 \), and an equation from the tangent plane to \(S\) at the point \((x_{0},y_{0},z_{0}) \) is

\( f_{x}(x_{0},y_{0})(x-x_{0}) +f_{y}(x_{0},y_{0})(y-y_{0}) - (z-z_{0}) = 0\).

Example 13.7.2 Finding an Equation for a Tangent Plane

Tangent plane to surface. Figure 13.7.4

Find an equation of the tangent plane to the hyperboloid \( z^{2}-2x^{2}-2y^{2} = 12 \) at the point \((1,-1,4)\). Solution Begin by writing the equation for the surface as \( z^{2}-2x^{2}-2y^{2} - 12 = 0. \) Consider \( F(x,y,z) = z^{2}-2x^{2}-2y^{2} - 12 \) which yields \( F_{x}(x,y,z) = -4x, \: F_{y}(x,y,z) = -4y \text{, and } F_{y}(x,y,z) = 2z.\) At the point \((1,-1,4)\), the partial derivatives are \( F_{x}(1,-1,4) = -4, \: F_{y}(1,-1,4) = 4 \text{, and } F_{y}(1,-1,4) = 8.\) An equation for the tangent line at \((1,-1,4)\) is \(0\) \(= -4(x-1)+4(y+1)+8(z-4) \) \(= -4x+4+4y+4+8z-32\) \(= -4x+4y+8z-24\) \(= x-y-2z+6.\) The semi-hyperboloid and the tangent plane are shown in Figure 13.7.4.

Example 13.7.3 Finding an Equation for a Tangent Plane Along the \(Z\)-Axis

Figure 13.7.5

Find the equation for the tangent plane to the paraboloid $$z=1-\frac{1}{10} (x^{2}+4y^{2}) $$ at the point \((1,1,\frac{1}{2})\). Solution Taking partial derivatives from the given equation produces \(f_{x}(x,y) \) $$= - \frac{x}{5} $$ \(\rightarrow\) \(f_{x}(1,1) \) $$= - \frac{1}{5} $$ \(f_{y}(x,y) \) $$= - \frac{4y}{5} $$ \(\rightarrow\) \(f_{y}(1,1) \) $$= - \frac{4}{5}. $$ An equation for the tangent plan at \((1,1,\frac{1}{2})\) is \(0\) $$= f_{x}(1,1)(x-1)+ f_{y}(1,1)(y-1)- \left( z - \frac{1}{2} \right) $$ $$= - \frac{1}{5}(x-1)- \frac{4}{5}(y-1)- \left( z - \frac{1}{2} \right)$$ $$= - \frac{1}{5}x- \frac{4}{5}y - z + \frac{3}{2} $$ as shown in Figure 13.7.5.

Example 13.7.4 Finding an Equation for a Normal Line to a Surface

Figure 13.7.6

Find the symmetric equations for the normal line to the surface \(xyz=12\) at the point \((2,-2,-3)\). Solution Let \(F(x,y,z) = xyz=12\). Then use the gradient to find the normal line. \( \nabla F(x,y,z) \) \(= F_{x}(x,y,z)\textbf{i} + F_{y}(x,y,z)\textbf{j} + F_{z}(x,y,z)\textbf{k} \) \(= yz\textbf{i} + xz\textbf{j} + xy\textbf{k} \) Now apply the point \((2,-2,-3)\), which yields \( \nabla F( \color{red}{2},\color{red}{-2},\color{red}{-3}) \) \(= (\color{red}{-2})(\color{red}{-3})\textbf{i} + (\color{red}{2})(\color{red}{-3})\textbf{j} + (\color{red}{2})(\color{red}{-2})\textbf{k} \) \(= 6\textbf{i} -6\textbf{j} -4\textbf{k}. \) The normal line at \((2,-2,-3)\) has direction numbers 6, -6, and -4, and the corresponding symmetric equations are $$ \frac{x-2}{6} = \frac{y+2}{-6} = \frac{z+3}{-4},$$ as shown in Figure 13.7.6.

Example 13.7.5 Finding an Equation for a Normal Line to a Surface In Three Dimensions

Figure 13.7.7

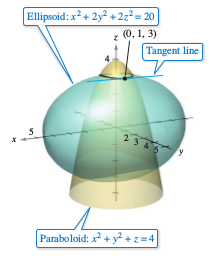
Describe the tangent line where the curve and ellipsoid intersect, \( x^{2}+2y^{2}+2z^{2} \) \(= 20 \:\:\:\: \) Ellipsoid \( x^{2}+y^{2}+z \) \(= 4\) Paraboloid at the point \((0,1,3)\), as shown in Figure 13.7.7. Solution Begin by finding the gradients to both surfaces at the point \((0,1,3)\). Ellipsoid Paraboloid \(F(x,y,z)\) \(= x^{2}+2y^{2}+2z^{2} -20\:\:\:\: \) \(G(x,y,z) \) \(=x^{2}+y^{2}+z -4 \) \( \nabla F(x,y,z)\) \(= 2x \textbf{i} + 4y \textbf{j} + 4z \textbf{k} \) \( \nabla G(x,y,z)\) \(= 2x \textbf{i} + 2y \textbf{j} + \textbf{k} \) \( \nabla F(0,1,3)\) \(= 4\textbf{j} + 12\textbf{k}\) \(\nabla G(0,1,3) \) \(= 2\textbf{j} + \textbf{k}\) The cross product for the gradients is a vector that is tangent to both surfaces at the point \((0,1,3)\). $$ \nabla F(0,1,3) \times \nabla G(0,1,3) = \begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ 0 & 4 & 12\\ 0 & 2 & 1 \end{vmatrix} = -20 \textbf{i}$$ Therefore, the tangent line to the curve intersecting both surfaces at the point \((0,1,3)\) is a line that is parallel to the \(x\)-axis and passes through the point \((0,1,3)\), as shown in Figure 13.7.7.

The Inclination Angle for a Plane

Inclination Angle Figure 13.7.8

Gradients can be used to find the inclination angle for a tangent plane to a surface. The inclination angle for a plane is defined as the angle \(\theta \:(0 \leqslant \theta \leqslant \pi/2)\) between the given plane and the \(xy\)-plane, as shown in Figure 13.7.8. The inclination angle for a horizontal plane is defined as zero. Because the vector \(\textbf{k}\) is normal to the \(xy\)-plane, the cosine formula for the angle between two planes, Section 11.5, can be used to conclude that the inclination angle for a plane with the normal vector \(\textbf{n}\) is $$ \cos \theta = \frac{| \textbf{n} \cdot \textbf{k}|}{\|\textbf{n}\|\| \textbf{k}\|} = \frac{| \textbf{n} \cdot \textbf{k}|}{\|\textbf{n}\|} \:\:\:\: \color{red}{ \text{Inclination Angle for a Plane}}$$

Example 13.7.6 Finding the Inclination Angle for a Tangent Plane

Inclination Angle Figure 13.7.9

Find the inclination angle for the tangent plane to the ellipsoid $$ \frac{x^{2}}{12} + \frac{y^{2}}{12} + \frac{z^{2}}{3} = 1$$ at the point \((2,2,1)\). Solution Let $$F(x,y,z) = \frac{x^{2}}{12} + \frac{y^{2}}{12} + \frac{z^{2}}{3} - 1.$$ Calculating the gradient for \(F\) at the point \((2,2,1)\) is \( \nabla F(x,y,z) \) $$= \frac{x}{6}\textbf{i} + \frac{y}{6}\textbf{j} + \frac{2z}{3}\textbf{k} $$ \( \nabla F(2,2,1) \) $$= \frac{1}{3}\textbf{i} + \frac{1}{3}\textbf{j} + \frac{2}{3}\textbf{k}. $$ Because \( \nabla F(2,2,1) \) is normal to the tangent plane and \( \textbf{k} \) is normal to the \(xy\)-plane, it follows that the inclination angle for the tangent plane is $$ \cos \theta = \frac{|\nabla F(2,2,1) \cdot \textbf{k} |}{\| \nabla F(2,2,1) \|} = \frac{2/3}{\sqrt{(1/3)^{2} +(1/3)^{2} + (2/3)^{2}}} = \sqrt{\frac{2}{3}} $$ which implies that $$\theta = \arccos \sqrt{\frac{2}{3}} \approx 35.3^{\circ}, $$ as shown in Figure 13.7.9. An alternative formula for the inclination angle \( \theta \) for the tangent plane to the surface \(z=f(x,y)\) at \((x_{0},y_{0},z_{0})\) is $$ \cos \theta = \frac{1}{\sqrt{[f_{x}(x_{0},y_{0})]^{2} + [f_{y}(x_{0},y_{0})]^{2} +1}} . $$

Comparison Between Gradients \(\nabla f(x,y)\) and \(\nabla F(x,y,z)\)

The discussion so far has shown that the gradient for a function \(f\) with two variables is normal to the level curves for \(f\). Theorem 13.6.3 states that if \(f\) is differentiable at \((x_{0},y_{0})\) and \(\nabla f(x_{0},y_{0}) \ne \textbf{0}\), the \(\nabla f(x_{0},y_{0})\) is normal to the level curve throughout \((x_{0},y_{0})\). This result is easily extended to functions with three variables.

Theorem 13.7.2 Gradient Is Normal to Level Surfaces

If \(F\) is differentiable at \((x_{0},y_{0},z_{0})\) and

\(\nabla F(x_{0},y_{0},z_{0}) \ne \textbf{0}\)

then \(\nabla F(x_{0},y_{0},z_{0}) \) is normal to the level surface through \((x_{0},y_{0},z_{0})\).

Internal Links

Parent Article: Calculus III 13 Functions with Several Variables