Calculus III 15.05 Parametric Surfaces

Previous	Calculus III 15.04 Green’s Theorem
Next	Calculus III 15.06 Surface Integrals

15.05 Parametric Surfaces

• Parametric surface definition
• Sketch a parametric surface.
• A parametric equation set to describe a surface.
• Find a normal vector and a tangent plane to a parametric surface.
• Find the area for a parametric surface.

Parametric Surfaces

Definition 15.5.1 Parametric Surfaces

For curves, note that the vector-valued function \(\textbf{r}\) is a function with a single parameter \(t\). For surfaces, the vector-valued function is a function with two parameters \(u\) and \(v\).

Let \(x\), \(y\), and \(z\) be functions for \(u\) and \(v\) that are continuous on a domain \(D\) in the \(uv\)-plane. The point set \((x,y,z)\) given by

\(\textbf{r}(u,v)=x(u,x)\textbf{i}+y(u,v)\textbf{j}+z(u,v)\textbf{k}\)	Parametric surface
is called a parametric surface. The equations
\(x=x(u,x)\), \(y=y(u,x)\), and \(z=z(u,x) \)	Parametric equations

are the parametric equations for the surface.

If \(S\) is a parametric surface given by the vector-valued function \(\textbf{r}\), then \(S\) is traced out by the position vector \(\textbf{r}(u,v)\) as the point \((u,v)\) moves through the domain \(D\), as shown in Figure 15.5.1.

Figure 15.5.1

Example 15.5.1 Sketching a Parametric Surface for a Cylinder

Figure 15.5.2

Identify and sketch the parametric surface \(S\) given by \(\textbf{r}(u,v)= 3 \cos u \textbf{i} + 3 \sin u\textbf{j}+v\textbf{k} \) where \(0 \leqslant u \leqslant 2\pi\) and \(0 \leqslant v \leqslant 4\). Solution Because \(x=3 \cos u\) and \(y=3 \sin u\) each point \((x,y,z)\) on the surface \(x\) and \(y\) are related by the equation \(x^{2}+y^{2}=3^{2}.\) Each cross section for \(S\) is a circle with radius 3 and centered on the \(z\)-axis and parallel to the \(xy\)-plane. Because \(z=v\) where \(0 \leqslant v \leqslant 4\) the surface is a right circular cylinder with height 4, as shown in Figure 15.5.1.

Example 15.5.2 Sketching a Parametric Surface for a Sphere

Figure 15.5.3

Identify and sketch the parametric surface \(S\) given by \(\textbf{r}(u,v)= \sin u \cos v \textbf{i} + \sin u \sin v\textbf{j}+ \cos u\textbf{k} \) where \(0 \leqslant u \leqslant \pi\) and \(0 \leqslant v \leqslant 2\pi\). Solution As with parametric representations for curves, parametric representations for surfaces are not unique. For this example, trigonometric identities will be used to eliminate the parameters. \(x^{2}+y^{2}+z^{2} \) \(=( \sin u \cos v)^{2} + (\sin u \sin v)^{2}+ (\cos u)^{2} \) \(= \sin^{2}u \cos^{2}v + \sin^{2}u \sin^{2}v + \cos^{2} u\) \(= \sin^{2} u( \cos^{2} v + \sin^{2} v) +\cos^{2} u \) \(= \sin^{2} u + \cos^{2} u = 1.\) Each point on \(S\) lies on the unit sphere, centered at the origin, as shown in Figure 15.5.3. For fixed \(u=d_{i}\), \(\textbf{r}(u,v)\) traces out latitude circles \(x^{2} + y^{2}= \sin^{2} d_{i}\), \(0 \leqslant d_{i} \leqslant \pi\) that are parallel to the \(xy\)-plane, and for fixed \(v=c_{i}\), \(\textbf{r}(u,v)\) traces out longitude, or meridian, half-circles. As proof that \(\textbf{r}(u,v)\) traces out the entire unit sphere, recall that the parametric equations \(x= \rho \sin \phi \cos \theta\), \(y= \rho \sin \phi \sin \theta\), and \(z=\rho \cos \phi\) where \(0 \leqslant \theta \leqslant2\pi \) and \(0 \leqslant \phi \leqslant \pi\), describe the conversion between spherical and rectangular coordinates, as discussed in Section 11.7.

Finding Parametric Equations for Surfaces

Examples 15.5.1 and 15.5.2 sketched a surface described by a parametric equation set. The reverse problem - deducing a parametric equation set for a given surface - is generally more difficult. For a surface type described by \(z=f(x,y)\), this problem is straightforward. The parametrized version is

\(\textbf{r}(x,y)= x\textbf{i}+y\textbf{j}+f(x,y)\textbf{k}\).

Example 15.5.3 Representing a Surface Parametrically

Figure 15.5.4

Write a parametric equation set for the cone given by \(z=\sqrt{x^{2}+y^{2}}\) as shown in Figure 15.5.4. Solution Because this surface has the form \(z=f(x,y)\), let \(x\) and \(y\) be the parameters. The cone's vector-valued function translates to \(\textbf{r}(x,y)= x\textbf{i}+y\textbf{j}+\sqrt{x^{2}+y^{2}}\textbf{k}\) where \((x,y)\) varies over the entire \(xy\)-plane.

A second surface that is easily represented parametrically is a rotated surface. For example, to represent the surface formed by revolving the graph for

\( y=f(x) \: a \leqslant x \leqslant b\)

about the \(x\)-axis, use

\(x=u, \: y=f(u) \cos v \text{, and } z=f(u) \sin v\)

where \(a \leqslant u \leqslant b\) and \( 0 \leqslant v \leqslant 2 \pi\).

The surface for Gabriel's Horn in Example 15.5.4 is formed by revolving the graph for \(y=f(x)\) about the \(x\)-axis. For other rotated surfaces a similar parametrization can be used. For example, to parametrize the surface formed by revolving the graph for \(x=f(z)\) about the \(z\)-axis, use

\(z=u, \: x=f(u) \cos v \text{, and } y=f(u) \sin v.\)

Example 15.5.4 Representing a Rotated Surface Parametrically

Figure 15.5.5

Write a parametric equation set for the rotated surface produced by revolving $$ f(x)=\frac{1}{x}, \: 1 \leqslant x \leqslant 10 $$ about the \(x\)-axis. Solution Use the parameters \(u\) and \(v\) as described above to write $$x=u, \: y=f(u) \cos v = \frac{1}{u} \cos v \text{, and } z=f(u) \sin v = \frac{1}{u} \sin v $$ where \( 1\leqslant u \leqslant 10 \text{ and } 0 \leqslant v \leqslant 2\pi.\) The resulting surface is the exterior for Gabriel's Horn, as shown in Figure 15.5.5.

Normal Vectors and Tangent Planes

Figure 15.5.6

Let \(S\) be a parametric surface given by \( \textbf{r}(u,v)=x(u,v)\textbf{i} + y(u,v)\textbf{j}+z(u,v)\textbf{k}\) over an open region \(D\) such that \(x\), \(y\), and \(z\) have continuous partial derivatives on \(D\). The partial derivatives for \( \textbf{r}\) with respect to \(u\) and \(v\) are defined as $$\textbf{r}_{u}= \frac{\partial x}{\partial u}(u,v)\textbf{i} + \frac{\partial y}{\partial u}(u,v)\textbf{j} + \frac{\partial z}{\partial u}(u,v)\textbf{k}$$ and $$\textbf{r}_{v}= \frac{\partial x}{\partial v}(u,v)\textbf{i} + \frac{\partial y}{\partial v}(u,v)\textbf{j} + \frac{\partial z}{\partial v}(u,v)\textbf{k}.$$ Each partial derivative is a vector-valued function that can be interpreted geometrically in as a tangent vector. For example, if \(v=v_{0}\) is held constant, then \( \textbf{r}(u,v_{0})\) is a vector-valued function for a single parameter and defines a curve \(C_{1}\) that lies on the surface \(S\). The tangent vector to \(C_{1}\) at the point \( (x(u_{0},v_{0}), y(u_{0},v_{0}), z(u_{0},v_{0}))\) is given by $$\textbf{r}_{u}(u_{0},v_{0})= \frac{\partial x}{\partial u}(u_{0},v_{0})\textbf{i} + \frac{\partial y}{\partial u}(u_{0},v_{0})\textbf{j} + \frac{\partial z}{\partial u}(u_{0},v_{0})\textbf{k}$$ as shown in Figure 15.5.6. Similarly, if \(u=u_{0}\) is held constant, the \(\textbf{r}(u_{0},v)\) is a vector valued function with a single parameter and defines a curve \(C_{2}\) that lies on the surface \(S\). The tangent vector to \(C_{2}\) at the point \( (x(u_{0},v_{0}), y(u_{0},v_{0}), z(u_{0},v_{0}))\) is given by $$\textbf{r}_{v}(u_{0},v_{0})= \frac{\partial x}{\partial v}(u_{0},v_{0})\textbf{i} + \frac{\partial y}{\partial v}(u_{0},v_{0})\textbf{j} + \frac{\partial z}{\partial v}(u_{0},v_{0})\textbf{k}.$$ If the normal vector \(\textbf{r}_{u} \times \textbf{r}_{v} \) is not \(\textbf{0}\) for any \((u,v)\) in \(D\), then the surface \(S\) is called smooth and will have a tangent plane. Informally, a smooth surface is one that has no sharp points or cusps. For instance, spheres, ellipsoids, and paraboloids are smooth, whereas the cone given in Example 15.5.3 is not smooth.

Definition 15.5.2 Normal Vector to a Smooth Parametric Surface

Let \(S\) be a smooth parametric surface

\(\textbf{r}(u,v) = x(u,v)\textbf{i} +y(u,v)\textbf{j} +z(u,v)\textbf{k} \)

defined over an open region \(D\) in the \(uv\)-plane. Let \((u_{0},v_{0})\) be a point in \(D\). A normal vector at the point

\((x_{0},y_{0},z_{0}) = (x(u_{0},v_{0}), y(u_{0},v_{0}), z(u_{0},v_{0}))\)

is given by

$$ \textbf{N} = \textbf{r}_{u}(u_{0},v_{0}) \times \textbf{r}_{v}(u_{0},v_{0}) = \begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & \frac{\partial z}{\partial u} \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & \frac{\partial z}{\partial v} \end{vmatrix}. $$

Figure 15.5.6 shows the normal vector \( \textbf{r}_{u} \times \textbf{r}_{v}\). It is also normal to \(S\) and points in the opposite direction.

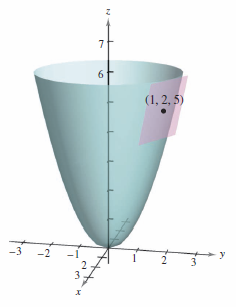
Example 15.5.5 Finding a Tangent Plane to a Parametric Surface

Figure 15.5.7

Find an equation for the tangent plane to the paraboloid \( \textbf{r}(u,v) = u\textbf{i} +v\textbf{j} +(u^{2}+v^{2})\textbf{k}\) at the point \((1,2,5)\). Solution The point in the \(uv\)-plane that maps to the point \((x,y,z)=(1,2,5)\) is \((u,v)=(1,2)\). The partial derivatives for \( \textbf{r}\) are \( \textbf{r}_{u} = \textbf{i} +2u\textbf{k} \) and \( \textbf{r}_{v} = \textbf{j} +2v\textbf{k}.\) The normal vector is given by $$\textbf{r}_{u} \times \textbf{r}_{v} =\begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ 1 & 0 & 2u \\ 0 & 1 & 2v \end{vmatrix} = -2u\textbf{i} -2v\textbf{j} +\textbf{k} $$ which implies that the normal vector at \((1,2,5)\) is \( -2(x-1) -4(y-2) + (z-5)\) \(= 0 \) \( -2x-4y+z\) \(=-5. \) The tangent plane is shown in Figure 15.5.7.

Area for a Parametric Surface

Figure 15.5.8

The techniques for determining surface area described in Section 14.5 can be extended to a parametric surface. Begin by constructing an inner partition on \(D\) having \(n\) rectangles, where the \(i\)th rectangle \(D_{i}\) is \(\Delta A_{i} = \Delta u_{i} \Delta v_{i}\), as shown in Figure 15.5.8. In each \(D_{i}\), let \((u_{i},v_{i})\) be that point closest to the origin. At the point \((x_{i},y_{i},z_{i}) = (x(u_{i},v_{i}),y(u_{i},v_{i}),z(u_{i},v_{i})) \) on the surface \(S\), construct a tangent plane \(T_{i}\). The area for the rectangle that corresponds to \(D_{i}\), \(T_{i}\), can be approximated by a parallelogram in the tangent plane. As in, \(\Delta T_{i} \approx \Delta S_{i}\). The surface for \(S\) is given by \(\sum \Delta S_{i} \approx \sum \Delta T_{i}\). The area for the parallelogram in the tangent plane is \( \| \Delta u_{i} \textbf{r}_{u} \times \Delta v_{i} \textbf{r}_{v} \| = \| \textbf{r}_{u} \times \textbf{r}_{v} \|\Delta u_{i} \Delta v_{i}\) which leads to Definition 15.5.3. Definition 15.5.3 Area for a Parametric Surface Let \(S\) be a smooth parametric surface \(\textbf{r}(u,v) = x(u,v)\textbf{i} +y(u,v)\textbf{j} +z(u,v)\textbf{k} \) defined over an open region \(D\) in the \(uv\)-plane. If each point on the surface \(S\) corresponds to exactly one point in the domain \(D\), then the surface area for \(S\) is given by $$\text{Surface area }= \int_{S} \int \: dS = \int_{D} \int \| \textbf{r}_{u} \times \textbf{r}_{v} \| \: dA$$ where $$\textbf{r}_{u}= \frac{\partial x}{\partial u}\textbf{i} + \frac{\partial y}{\partial u}\textbf{j} + \frac{\partial z}{\partial u}\textbf{k} \: \text{ and } \: \textbf{r}_{v}= \frac{\partial x}{\partial v}\textbf{i} + \frac{\partial y}{\partial v}\textbf{j} + \frac{\partial z}{\partial v}\textbf{k}.$$ A surface \(S\) given by \(z=f(x,y)\) can be parametrized using the vector valued function \(\textbf{r}(x,y) = x\textbf{i} +y\textbf{j} +f(x,y)\textbf{k} \) defined over the region \(R\) in the \(xy\)-plane. Using \(\textbf{r}_{x} = \textbf{i} + f_{x}(x,y)\textbf{k}\) and \(\textbf{r}_{y} = \textbf{j} + f_{y}(x,y)\textbf{k}\) produces $$\textbf{r}_{x} \times \textbf{r}_{y} =\begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ 1 & 0 & f_{x}(x,y) \\ 0 & 1 & f_{y}(x,y)\end{vmatrix}= -f_{x}(x,y)\textbf{i} -f_{y}(x,y) \textbf{j} + \textbf{k}$$ and \( \| \textbf{r}_{x} \times \textbf{r}_{y} \| = \sqrt{[f_{x}(x,y)]^{2}+[f_{y}(x,y)]^{2}} .\) This produces the surface area for \(S\) as \(\text{Surface area }\) $$= \int_{R} \int \| \textbf{r}_{x} \times \textbf{r}_{y} \| \: dA $$ $$= \int_{R} \int \sqrt{[f_{x}(x,y)]^{2}+[f_{y}(x,y)]^{2}} \: dA.$$

Example 15.5.6 Surface Area for a Sphere

Find the surface area for the unit sphere

\(\textbf{r}(u,v) = \sin u \cos v\textbf{i} + \sin u \sin v\textbf{j} + \cos u\textbf{k} \)

where the domain \(D\) is \(0 \leqslant u \leqslant \pi \) and \( 0 \leqslant v \leqslant 2 \pi\).
Solution Calculating \(\textbf{r}_{u}\) and \(\textbf{r}_{v}\) produces

\(\textbf{r}_{u} \)	\(= \cos u \cos v\textbf{i} + \cos u \sin v\textbf{j} - \sin u\textbf{k} \)
\(\textbf{r}_{v} \)	\(= -\sin u \sin v\textbf{i} + \sin u \cos v\textbf{j}. \)

Their cross produce is

\(\textbf{r}_{u} \times \textbf{r}_{v} \)	$$= \begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ \cos u \cos v & \cos u \sin v & -\sin u\\ -\sin u \sin v & \sin u \cos v & 0\end{vmatrix}$$
	\(= \sin^{2}u \cos v\textbf{i} + \sin^{2} u \sin v \textbf{j} + \sin u \cos u \textbf{k} \)

Normalizing the cross product produces

\( \| \textbf{r}_{u} \times \textbf{r}_{v} \|\)	\(= \sqrt{(\sin^{2}u \cos v)^{2} + (\sin^{2} u \sin v)^{2} + (\sin u \cos u)^{2}}\)
	\(= \sqrt{\sin^{4} u + \sin^{2}u \cos^{2}u }\)
	\(= \sqrt{\sin^{2} u }\)
	\(= \sin u. \:\:\:\: \color{red}{ \sin u > 0 \text{ for } 0 \leqslant u \leqslant \pi} \)

Integrating the normalized cross product produces the sphere's surface area

\(A\)	$$=\int_{D} \int \| \textbf{r}_{u} \times \textbf{r}_{v} \| \: dA $$
	$$= \int_{0}^{2\pi} \int_{0}^{\pi} \sin u \: du \: dv $$
	$$= \int_{0}^{2\pi} 2 \: dv = 4 \pi.$$

Note: This surface does not satisfy the requirement in Definition 15.5.3 that each point on the surface corresponds to exactly one point in \(D\) because \( \textbf{r}(u,0) = \textbf{r}(u,2\pi) \) for any fixed value for \(u\). However, because the overlap is only a semicircle with no area, the definition can be applied.

Example 15.5.7 Finding the Surface area for a Torus

Figure 15.5.9

Find the surface area for the torus given by \(\textbf{r}(u,v) = (2+ \cos u) \cos v\textbf{i} + (2+\cos u) \sin v\textbf{j} + \sin u\textbf{k} \) where the domain \(D\) is \(0 \leqslant u \leqslant \pi \) and \( 0 \leqslant v \leqslant 2 \pi\), as shown in Figure 15.5.9. Solution Calculating \(\textbf{r}_{u}\) and \(\textbf{r}_{v}\) produces \(\textbf{r}_{u} \) \(= -\sin u \cos v\textbf{i} - \sin u \sin v\textbf{j} + \cos u\textbf{k} \) \(\textbf{r}_{v} \) \(= -(2+ \cos u) \sin v\textbf{i} + (2+ \cos u) \cos v\textbf{j}. \) Their cross produce is \(\textbf{r}_{u} \times \textbf{r}_{v} \) $$= \begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ -\sin u \cos v & -\sin u \sin v & \cos u\\ -(2+ \cos u) \sin v & (2+ \cos u) \cos v & 0\end{vmatrix}$$ \(= -(2+ \cos u) (\cos v \cos u \textbf{i} + \sin v \cos u \textbf{j} + \sin u \textbf{k}) \) Normalizing the cross product produces \( \| \textbf{r}_{u} \times \textbf{r}_{v} \|\) \(= (2+ \cos u)\sqrt{(\cos v \cos u)^{2} + (\sin v \cos u)^{2} + (\sin u )^{2}}\) \(= (2+ \cos u) \sqrt{\cos^{2} u (\cos^{2} v + \sin^{2} v) + \sin^{2} u }\) \(= (2+ \cos u)\sqrt{\cos^{2} u + \sin^{2} u}\) \(= 2+ \cos u.\) Integrating the normalized cross product produces the sphere's surface area \(A\) $$=\int_{D} \int \| \textbf{r}_{u} \times \textbf{r}_{v} \| \: dA $$ $$= \int_{0}^{2\pi} \int_{0}^{2\pi} (2+ \cos u) \: du \: dv $$ $$= \int_{0}^{2\pi} 4 \pi \: dv = 8 \pi^{2}.$$

The formula discussed in Section 7.4.3 is equivalent Definition 15.5.3. For example, suppose that \(f\) is a nonnegative function such that \(f^{\prime}\) is continuous over the interval \([a,b]\). Let \(S\) be the rotated surface formed by revolving the graph for \(f\), where \( a \leqslant x \leqslant b\), about the \(x\)-axis. The formula in Section 7.4.3 is

$$\text{Surface area } = 2 \pi \int_{a}^{b} f(x) \sqrt{1 + [f^{\prime}(x)]^{2}}. $$

To represent \(S\) parametrically, let

\(x=u, \: y=f(u) \cos v \text{, and } z = f(u) \sin v\)

where \(a \leqslant u \leqslant b \) and \( 0 \leqslant v \leqslant 2 \pi.\) Then,

\(\textbf{r}(u,v) = u \textbf{i} + f(u) \cos v\textbf{j} + f( u) \sin v \textbf{k}.\)

Internal Links

Parent Article: Calculus III 15 Vector Analysis