Calculus III 15.08 Stokes’s Theorem

Previous

Calculus III 15.07 Divergence Theorem

15.08 Stokes’s Theorem[1]

• Understand and use Stokes's Theorem
• Use curl to analyze the motion for a rotating liquid.

Stokes's Theorem

Figure 15.8.1 Figure 15.8.2

A second higher-dimension analog to Green’s Theorem is called Stokes’s Theorem, after the English mathematical physicist George Gabriel Stokes[2]. Stokes belonged to the "Cambridge School" along with William Thomson (Lord Kelvin) and James Clerk Maxwell at the University of Cambridge[3]. In addition to making contributions to physics, Stokes worked with infinite series and differential equations, as well as with the integration results discussed here. Stokes’s Theorem describes the relationship between a surface integral over an oriented surface \(S\) and a line integral along a closed three-dimensional curve \(C\) forming the boundary for \(S\), as shown in Figure 15.8.1. The positive direction along \(C\) is counterclockwise relative to the normal vector \( \textbf{N}\). That is, if you imagine grasping the normal vector \( \textbf{N}\) with your right hand, with your thumb pointing in the \( \textbf{N}\)'s direction, your fingers will point in the positive direction \(C\), as shown in Figure 15.8.2. This is a variant on the Right Hand Rule[4]. Theorem 15.8.1 Stokes's Theorem Let \(S\) be an oriented surface with unit normal vector \( \textbf{N}\), bounded by a piecewise smooth simple closed curve \(C\) with a positive orientation. If \( \textbf{F}\) is a vector field whose component functions have continuous first partial derivatives on an open region containing \(S\) and \(C\), then $$ \int_{C} \textbf{F} \cdot \:d \textbf{r} = \int_{S} \int (\text{curl} \: \textbf{F}) \cdot \textbf{N} \: dS. $$ Note that the line integral may be written in the differential form $$ \int_{C} M \:dx + N \: dy + P \: dz$$ or in the vector form $$ \int_{C} \textbf{F} \cdot \textbf{T} \: ds.$$

Example 15.8.1 Using Stokes's Theorem

Figure 15.8.3

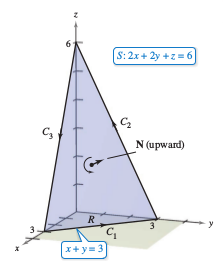
Let \(C\) be the oriented triangle lying in the plane \(2x+2y+z=6\) as shown in Figure 15.8.3. Evaluate $$ \int_{C} \textbf{F} \cdot \: d\textbf{r}$$ where \( \textbf{F} (x,y,z) = -y^{2}\textbf{i}+z\textbf{j}+x\textbf{k}.\) Solution Apply Stokes's Theorem by finding the curl for \(\textbf{F}\). $$ \text{curl} \: \textbf{F}= \begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ -y^{2} & z & x\end{vmatrix} = -\textbf{i}-\textbf{j}+2y\textbf{k} $$ Considering \(z=g(x,y)=6-2x-2y\) Theorem 15.8.1 can be applied for an upward normal vector to produce $$ \int_{C} \textbf{F} \cdot \: d\textbf{r}$$ $$= \int_{S} \int (\text{curl} \: \textbf{F}) \cdot \textbf{N} \: dS$$ $$= \int_{R} \int (-\textbf{i}-\textbf{j}+2y\textbf{k}) \cdot [-g_{x}(x,y)\textbf{i}-g_{y}(x,y)\textbf{j}+\textbf{k}] \:dA $$ $$=\int_{R} \int (-\textbf{i}-\textbf{j}+2y\textbf{k}) \cdot (2\textbf{i}+2\textbf{j}+\textbf{k}) \:dA $$ $$=\int_{0}^{3} \int_{0}^{3-y} (2y-4) \:dx \:dy $$ $$= \int_{0}^{3} (-2y^{2}+10y-12) \: dy$$ $$= \left[ \frac{2y^{3}}{3} + 5y^{2}-12y \right]_{0}^{3} = -9. $$

Try evaluating the line integral in Example 15.8.1 directly, without using Stokes's Theorem. One way to do this would be to consider \(C\) as the union between \(C_{1}\), \(C_{2}\), and \(C_{3}\), as follows.

\(C_{1}: \: \textbf{r}_{1}(t) \)	\(= (3-t)\textbf{i}+t\textbf{j}, \: 0 \leqslant t \leqslant 3 \)
\(C_{2}: \: \textbf{r}_{2}(t) \)	\(= (6-t)\textbf{j}+(2t-6)\textbf{k}, \: 3 \leqslant t \leqslant 6 \)
\(C_{3}: \: \textbf{r}_{3}(t) \)	\(= (t-6)\textbf{i}+(18-2t)\textbf{k}, \: 6 \leqslant t \leqslant 9 \)

The evaluation works out as

$$ \int_{C} \textbf{F} \cdot \: d\textbf{r} $$	$$=\int_{C_{1}} \textbf{F} \cdot \textbf{r}_{1}^{\prime}(t) \: dt + \int_{C_{2}} \textbf{F} \cdot \textbf{r}_{2}^{\prime}(t) \: dt + \int_{C_{3}} \textbf{F} \cdot \textbf{r}_{3}^{\prime}(t) \: dt $$
	$$=\int_{0}^{3} t^{2} \: dt + \int_{3}^{6} (-2t+6) \: dt +\int_{6}^{9} (-2t+12) \: dt $$
	$$=9-9-9 = -9. $$

Example 15.8.2 Verifying Stokes's Theorem

Figure 15.8.4

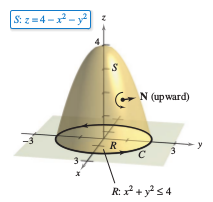
Consider the paraboloid \(S\) described by \(z=4-x^{2}-y^{2}\) lying above the \(xy\)-plane and oriented upward, as shown in Figure 15.8.4. Let \(C\) be its boundary curve in the \(xy\)-plane, oriented counterclockwise. Verify Stokes's Theorem for \( \textbf{F} (x,y,z) = 2z\textbf{i}+x\textbf{j}+y^{2}\textbf{k}\) by evaluating the surface integral and the equivalent line integral. Solution As a surface integral the partial derivatives are \(z=g(x,y) = 4 - x^{2}-y^{2} \), \(g_{x}=-2x\), \(g_{y}=-2y\), and $$ \text{curl} \: \textbf{F}= \begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ 2z & x & y^{2}\end{vmatrix} = 2y\textbf{i}+2\textbf{j}+\textbf{k}.$$ Applying Theorem 15.8.1 produces $$\int_{S} \int (\text{curl} \: \textbf{F}) \cdot \textbf{N} \: dS $$ $$=\int_{R} \int (2y\textbf{i}+2\textbf{j}+\textbf{k}) \cdot (2x\textbf{i}+2y\textbf{j}+\textbf{k}) \:dA $$ $$= \int_{-2}^{2} \int_{-\sqrt{4-x^{2}}}^{\sqrt{4-x^{2}}} (4xy+4y+1) \: dy \: dx $$ $$=\int_{-2}^{2} \left[ \vphantom{\frac{1}{2}} 2xy^{2}+2y^{2}+y \right]_{-\sqrt{4-x^{2}}}^{\sqrt{4-x^{2}}} \: dx $$ $$=\int_{-2}^{2} 2 \sqrt{4-x^{2}} \: dx$$ \(=4\pi. \:\:\:\: \color{red}{ \text{Area for a circle with radius } 2} \) As a line integral \(C\) can be parametrized as \( \textbf{r} (t) = 2 \cos t\textbf{i}+ 2 \sin t\textbf{j}+0\textbf{k}, \: 0 \leqslant t \leqslant 2 \pi. \) For \( \textbf{F} (x,y,z) = 2z\textbf{i}+x\textbf{j}+y^{2}\textbf{k}\) produces $$ \int_{C} \textbf{F} \cdot \: d\textbf{r} $$ $$= \int_{C} M \: dx + N \: dy + P \: dz $$ $$= \int_{C} 2z+x+y^{2} \: dz$$ $$= \int_{0}^{2 \pi} [0 + 2 \cos t (2 \cos t) + 0] \: dt $$ $$= \int_{0}^{2 \pi} 4 \cos^{2} t \: dt $$ $$= 2 \int_{0}^{2 \pi} (1+\cos 2t) \: dt$$ $$=2 \left[ t + \frac{1}{2} \sin 2t \right]_{0}^{2 \pi} = 4 \pi. $$

Curl's Physical Interpretation

Figure 15.8.5 Figure 15.8.6

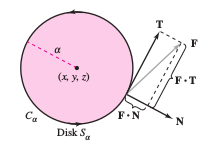
Stokes’s Theorem provides insight into a physical curl's interpretation. In a vector field \(\textbf{F}\), let \(S_{\alpha}\) be a small circular disk with radius \(\alpha\), centered at \((x,y,z)\) and with boundary \(C_{\alpha}\), as shown in Figure 15.8.5. At each point on the circle \(C_{\alpha}\), \(\textbf{F}\) has a normal component \(\textbf{F} \cdot \textbf{N}\) and a tangential component \(\textbf{F} \cdot \textbf{T}\). The more closely \(\textbf{F}\) and \( \textbf{N}\) are aligned, the greater the value for \(\textbf{F} \cdot \textbf{T}\). Therefore, a fluid tends to move along the circle rather than across it. This means the line integral around \(C_{\alpha}\) measures the circulation for \(\textbf{F}\) around \(C_{\alpha}\). As an equation, $$ \int_{C_{\alpha}} \textbf{F} \cdot \textbf{T} \:ds = \text{ circulation for }\textbf{F} \text{ around } C_{\alpha}.$$ Consider a small disk \(S_{\alpha}\) centered at some point \((x,y,z)\) on the surface \(S\), as shown in Figure 15.8.6. On such a small disk, curl \(\textbf{F} \) is nearly constant, because it varies little from its value at \((x,y,z)\). Moreover, curl \(\textbf{F} \cdot \textbf{N}\) is also nearly constant on \(S_{\alpha}\) because all unit normals to \(S_{\alpha}\) are about the same. Applying Stokes's Theorem yields $$ \int_{C_{\alpha}} \textbf{F} \cdot \textbf{T} \:ds $$ $$= \int_{S_{\alpha}} \int (\text{curl} \: \textbf{F}) \cdot \textbf{N} \:dS $$ $$\approx (\text{curl} \: \textbf{F}) \cdot \textbf{N} \int_{S_{\alpha}} \int \:dS $$ $$\approx (\text{curl} \: \textbf{F}) \cdot \textbf{N} (\pi \alpha^{2}).$$ This produces $$(\text{curl} \: \textbf{F}) \cdot \textbf{N}$$ $$\approx \frac{\int_{C_{\alpha}} \textbf{F} \cdot \textbf{T} \:ds}{\pi \alpha^{2}} $$ $$=\frac{\text{circulation for }\textbf{F} \text{ around } C_{\alpha}}{\text{disk area } S_{\alpha}} $$ \(=\: \) circulation rate. Assuming conditions are such that the approximation improves for smaller and smaller disks \((\alpha \rightarrow 0)\), if follows that $$ \text{curl} \: \textbf{F} \cdot \textbf{N} = \lim_{\alpha \rightarrow 0} \frac{1}{\pi \alpha^{2}} \int_{C_{\alpha}} \textbf{F} \cdot \textbf{T} \:ds$$ which is refered to as the rotation for \(\textbf{F}\) about \( \textbf{N} \). As an equation, \( \text{curl} \: \textbf{F} (x,y,z) \cdot \textbf{N} = \text{ rotation for } \textbf{F} \text{ about }\textbf{N} \text{ at } (x,y,z)\). In this case, the rotation for \(\textbf{F}\) is maximum when curl \(\textbf{F}\) and \(\textbf{N}\) have the same direction. Normally, this tendency to rotate will vary from point to point on the surface \(S\), and Stokes’s Theorem $$ \color{red}{\underbrace{\color{black}{\int_{C} \textbf{F} \cdot \:d \textbf{r}}}_{\color{red}{\text{Line Integral}}}} =\color{red}{\underbrace{\color{black}{ \int_{S} \int (\text{curl} \: \textbf{F}) \cdot \textbf{N} \: dS}}_{\color{red}{\text{Surface Integral}}}}.$$ says that the collective measure of this rotational tendency taken over the entire surface \(S\) (surface integral) is equal to the tendency for a fluid to circulate around the boundary \(C\) (line integral). If curl \( \textbf{F} =0 \) throughout region \(Q\), then the rotation for \(\textbf{F}\) about each unit normal \(\textbf{N}\) is zero. Therefore, \(\textbf{F}\) is irrotational. This is a characteristic for conservative vector fields.

Example 15.8.3 Curl Application

Figure 15.8.7 Figure 15.8.8

A liquid is swirling around in a cylindrical container with radius 2, so that its motion is described by the velocity field \( \textbf{F}(x,y,z) = -y\sqrt{x^{2}+y^{2}}\textbf{i} + x\sqrt{x^{2}+y^{2}}\textbf{j} \) as shown in Figure 15.8.7 and Figure 16.8.8. Find $$\int_{S} \int (\text{curl} \: \textbf{F}) \cdot \textbf{N} \: dS$$ where \(S\) is the upper surface for the cylindrical container. Solution The curl for \(\textbf{F}\) is given by $$ \text{curl} \: \textbf{F} =\begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ -y\sqrt{x^{2}+y^{2}} & x\sqrt{x^{2}+y^{2}} & 0\end{vmatrix} = 3 \sqrt{x^{2}+y^{2}}\textbf{k}.$$ Letting \(\textbf{N} = \textbf{k}\) produces $$\int_{S} \int (\text{curl} \: \textbf{F}) \cdot \textbf{N} \: dS $$ $$=\int_{R} \int 3 \sqrt{x^{2}+y^{2}} \: dA$$ $$= \int_{0}^{2 \pi} \int_{0}^{2} (3r)r \: dr \: d\theta$$ $$= \left. \int_{0}^{2 \pi} r^{3} \right]_{0}^{2} \: d\theta$$ $$= \int_{0}^{2 \pi} 8 \: d\theta = 16 \pi.$$

Summary 15.8.1 Integration Formulas

Fundamental Theorem of Calculus	Fundamental Theorem of Line Integrals
$$\int_{a}^{b} F^{\prime}(x) \:dx=F(b)-F(a) \:\:\:\:$$	$$ \int_{C} \textbf{F} \cdot \: d\textbf{r}= \int_{C} \nabla f \cdot \: d\textbf{r}= f(x(b),y(b)) - f(x(a),y(a))$$
Green’s Theorem
$$ \int_{C} M \: dx + N \: dy = \int_{R} \int \left(\frac{\partial N}{\partial x} -\frac{\partial M}{\partial y} \right) \:dA = \int_{C} \textbf{F} \cdot \textbf{T} \:ds = \int_{C} \textbf{F} \cdot \: d\textbf{r} = \int_{R} \int (\text{curl}\: \textbf{F} \cdot \textbf{k} \: dA $$
$$\int_{C} \textbf{F} \cdot \textbf{N} \:ds = \int_{R} \int \text{div}\: \textbf{F} \: dA$$
Divergence Theorem	Stokes's Theorem
$$ \int_{S} \int \textbf{F}) \cdot \textbf{N} \: dS = \int \int_{Q} \int \text{div}\: \textbf{F} \: dV$$	$$ \int_{C} \textbf{F} \cdot \:d \textbf{r} = \int_{S} \int (\text{curl} \: \textbf{F}) \cdot \textbf{N} \: dS$$

Internal Links

Parent Article: Calculus III 15 Vector Analysis