Calculus II 08.06 Integration by Tables and Other Integration Techniques
| Previous | Calculus II 08.05 Partial Fractions |
| Next | Calculus II 08.07 Indeterminate Forms and L’Hôpital’s Rule |
Contents
8.6 Integration by Tables and Other Integration Techniques
- Evaluate an indefinite integral using an integral table.
- Evaluate an indefinite integral using reduction formulas.
- Evaluate an indefinite integral involving rational sine and cosine functions.
Integration by Tables
Mathematics is about recognizing which rule to use in solving a problem. Slightly altering an integrand will require a different integration technique, or may not result in an elementary function, as shown below.
| $$ \int x \ln x \:dx $$ | $$= \frac{x^{2}}{4}\ln x - \frac{x^{2}}{4} + C \:\:\:\: $$ | Integration by parts |
| $$ \int \frac{ \ln x }{x} \:dx $$ | $$= \frac{(\ln x)^{2}}{2} + C $$ | Power Rule |
| $$ \int \frac{1}{x \ln x} \:dx $$ | $$= \ln|\ln x| + C$$ | Log Rule |
| $$ \int \frac{x}{\ln x} \:dx $$ | $$ =\:? $$ | Not an elementary function |
Integral Tables are just what they sound like. Proven integrals grouped by type. The first trick is matching the equation in question to the correct integral in the table. The second trick is rewriting the equation in question so that is does match an integral in the table.
Example 8.6.1 Integration by Tables Using Substitution
Find
- $$ \int \frac{dx}{ x\sqrt{x-1}} $$
Solution Rewrite the equation to
- $$ \int \frac{1}{ x\sqrt{x-1}}\:dx $$
The equation fits the integral \( \sqrt{a+bu} \) if we let \(a=-1\), \(b=1\), and \(u=x\) then \(dx=du\).
- $$x \sqrt{x-1} = u \sqrt{-1+1u} = \sqrt{a+bu} $$
Now the integral can be used.
- $$ \int \frac{1}{ u\sqrt{a+bu}} \:du = \frac{2}{\sqrt{-a}}\arctan \sqrt{\frac{a+bu}{-a}}+C$$
Back substitution produces
- $$ \int \frac{1}{ x\sqrt{x-1}}\:dx = 2\arctan \sqrt{x-1}+C.$$
Example 8.6.2 Integration by Tables with Rewriting the Equation
Find
- $$ \int x\sqrt{x^{4}-9}\:dx $$
Solution At first glance the equation matches no integral in the table. Rewrite \( \sqrt{x^{4}-9} \) as \( \sqrt{(x^{2})^{2}-3^{2}} \) and it matches \( \sqrt{u^{2}-a^{2}} \) in the integral
- $$ \int\sqrt{u^{2}-a^{2}} \:du = \frac{1}{2} \left ( u \sqrt{u^{2}-a^{2}} -a^{2} \ln \left|u+ \sqrt{u^{2}-a^{2}}\right| \right ) +C $$
except for that spare \(x\). The Power Rule allows us to integrate that spare \(x\) separately as \(x^{2}\).
Letting \(u=x^{2}\), \(a=3\), and \(du=2x\:dx\) produces
| $$ \int x\sqrt{x^{4}-9}\:dx $$ | $$= \frac{1}{2} \int \sqrt{(x^{2})^{2}-3^{2}} (2x)\:dx $$ | |
| $$ = \frac{1}{4} (x^{2} \sqrt{x^{4}-9} -9\ln |x^{2}+ \sqrt{x^{4}-9}|) +C \:\:\:\: $$ | Restore\( x \) as \(x^{2}\) |
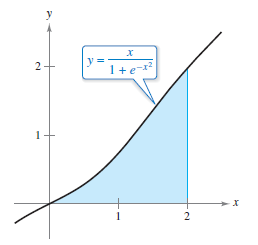
Example 8.6.3 Integration by Tables with Natural Logs
|
Evaluate
Solution Selecting from integrals with \(e^{u}\) this stands out
Letting \(u=-x^{2}\) and \(du = -2x\:dx\) produces
Back substitution produces
as shown in Figure 8.6.1. |
Reduction Formulas
Reduction Formulas express the integral as a function plus a simpler integral and have the form
- $$ \int f(x)\:dx = g(x) + \int h(x)\:dx. $$
Example 8.6.4 Using the Reduction Formula with \(\sec x\)
Find
- $$ \int \sec x^{3}\:dx $$
Solution Use the reduction formula
- $$ \int \sec x^{n}\:dx = \frac{\sec^{n-2}x\: \tan x}{n-1}+ \frac{n-2}{n-1} \int \sec^{n-2}x\:dx $$
where \(n=3\).
- $$ = \frac{1}{2} \int \sec x\:dx + \frac{1}{2}\sec x\: \tan x $$
The integral for \( \sec x \) is \( \log( \sec x + \tan x ) \).
- $$ = \frac{1}{2} \log ( \sec x + \tan x) + \frac{1}{2}\sec x\: \tan x + C$$
Rational Functions for Sine and Cosine
Example 8.6.5 Integration by Tables with Sine and Cosine
Find
- $$ \int \frac{\sin 2x}{2+\cos x}\:dx.$$
Solution No integral in the table matches the equation. Substituting \( 2 \sin x \cos x\) for \( \sin 2x\) produces
- $$ \int \frac{\sin 2x}{2+\cos x}\:dx = 2 \int \frac{\sin x \cos x}{2+\cos x}\:dx $$
which simplifies the equation. Looking for forms with \(a+bu\) produces
- $$ \int \frac{u}{a+bu}\:du = \frac{1}{b^{2}}(bu-a \ln|a+bu|) +C.$$
Letting \(a=2\), \(b=1\), \(u= \cos x\), and \(du= - \sin x\:dx\) produces
| $$ 2 \int \frac{\sin x \cos x}{2+\cos x}\:dx $$ | $$ = -2 \int \frac{ \cos x (-\sin x\:dx)}{2+\cos x} $$ |
| $$ = -2(\cos x -2 \ln|2+\cos x|) + C $$ | |
| $$ \large = -2\cos x +4 \ln|2+\cos x| + C $$ |
Definition 8.6.1 Substitution for Rational Functions with Sine and Cosine
For integrals involving rational functions with sine and cosine, the substitution
- $$ u= \frac{\sin x}{1+\cos x} = \tan \frac{x}{2} $$
yields
- $$ \cos x = \frac{1-u^{2}}{1+u^{2}} \text{, } \sin x = \frac{2u}{1+u^{2}}, \text{ and } dx=\frac{2\:du}{1+u^{2}}.$$
Proof From the substitution for \(u\), if follows that
- $$ u^{2}= \frac{\sin^{2} x}{(1+\cos x)^{2}} = \frac{1-\cos^{2} x}{(1+\cos x)^{2}} = \frac{1-\cos x}{1+\cos x}. $$
Solving for \( \cos x\) produces \( \cos x=(1-u^{2})/(1+u^{2})\). To find \( \sin x\), write \(u=\sin x/(1+ \cos x)\) as
- $$ \sin x = u(1+\cos x) =u \left ( 1+ \frac{1- u^{2} x}{1+ u^{2}} \right ) = \frac{2u}{1+ u^{2}}. $$
To find \(dx\) let \( u= \tan (x/2)\). Then \( \arctan u = x/2\) and
- $$dx = \frac{2\:du}{1+u^{2}}. $$
Example 8.6.6 Integration by Tables Using Substitution
Find
- $$ \int \frac{ \sin 2x }{2+ \cos x}\:dx$$
This form is not in the integration tables. Use special substitution to convert the trigonometric expression to a standard rational expression.
Solution Substituting \(2 \sin x \cos x\) for \(\sin 2x \) produces
- $$ \int \frac{ \sin 2x }{2+ \cos x}\:dx = 2 \int \frac{ \sin x \cos x}{2+ \cos x}\:dx .$$
Consider a form with \(a+bu\)
- $$ \int \frac{ u\:du }{a+bu}=\frac{1}{b^{2}} (bu - a \ln |a+bu|) + C.$$
Let \(a=2\), \(b=1\), and \(u=\cos x\). Then \(du=- \sin x \:dx\), this yields
| $$2 \int \frac{ \sin x \cos x}{2+ \cos x}\: dx $$ | $$= -2 \int \frac{ \cos x (-\sin x \:dx}{2+ \cos x} $$ |
| \(= -2 ( \cos x - 2 \ln | 2 + \cos x | ) + C\) | |
| \(= -2 \cos x - 4 \ln | 2 + \cos x | + C\) |
Internal Links
Parent Article: Calculus II 08 Integration Techniques