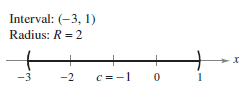Calculus II 09.08 Power Series

Previous	Calculus II 09.07 Taylor Polynomials and Approximations
Next	Calculus II 09.09 Using Power Series to Represent a Function

9.8 Power Series[1]

• Understand the definition for a power series.
• Find the radius and interval for power series' convergence.
• Determine the endpoint for a power series' convergence.
• Differentiate and integrate a power series.

Power Series

An infinite series called, a Power Series, can represent several important function types, like \(f(x)=e^{x}\), exactly. For example, the power series representation for \(f(x)=e^{x}\) is

$$e^{x} = 1+ x + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \cdots + \frac{x^{n}}{n!}+ \cdots.$$

For each real number \(x\), the infinite series on the right converges to the number \(e^{x}\). This leads to Definition 9.8.1.

Definition 9.8.1 Power Series

If \(x\) is a variable, then an infinite series with the form

$$ \sum_{n=0}^{\infty} a_{n}x^{n} = a_{0} + a_{1}x + a_{2}x^{2} + a_{3}x^{3} + \cdots + a_{n}x^{n} + \cdots $$

is called a power series. More generally, an infinite series with the form

$$ \sum_{n=0}^{\infty} a_{n}(x-c)^{n} = a_{0} + a_{1}(x-c) + a_{2}(x-c)^{2} + a_{3}(x-c)^{3} + \cdots + a_{n}(x-c)^{n} + \cdots $$

is called a power series centered at \(c\), where \(c\) is a constant.

Example 9.8.1 Power Series

a. The following power series is centered at 0.

$$ \sum_{n=0}^{\infty} \frac{x^{n}}{n!} = 1 + x + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \cdots $$

b. The following power series is centered at -1.

$$ \sum_{n=0}^{\infty} (-1)^{n}(x+1)^{n} = 1 - x + (x+1)^{1} + (x+1)^{2} - (x+1)^{3} + \cdots $$

c. The following power series is centered at 1.

$$ \sum_{n=0}^{\infty} \frac{1}{n}(x-1)^{n} = (x-1) + \frac{1}{2}(x-1)^{2} + \frac{1}{3} (x-1)^{3} + \cdots $$

Radius and Interval Convergence

Near \((c,f(c))\) the graph for \(P\) can be used to approximate the graph for \(f\). Figure 9.8.1

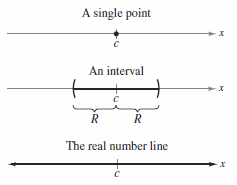
A power series can be viewed as a function, \(f(x)\) $$ f(x) = \sum_{n=0}^{\infty} a_{n}(x-c)^{n} $$ where the domain for \(f\) is the set for all \(x\) for which the power series converges. Determining the domain for a power series is critical in finding an exact value for \(f(x)\). In the trivial case every power series converges at its center \(c\) because $$ f(c) $$ $$= \sum_{n=0}^{\infty} a_{n}(c-c)^{n}$$ $$= a_{0}(1)+0+0+ \cdots +0+ \cdots$$ $$= a_{0}$$ Therefore, \(c\) always lies in the domain for \(f\). Theorem 9.8.1 states that the domain for a power series can take three basic forms: a single point, an interval centered at or the entire real number line, as shown in Figure 9.8.1.

Theorem 9.8.1 Convergence for a Power Series

For a power series centered at \(c\), precisely one among three features is true. 1. The series converges only at \(c\).
2. There exists a real number \(R > 0\) such that the series converges absolutely for

$$|x-c|<R $$

and diverges for

$$|x-c|>R $$

3. The series converges absolutely for all \(x\).
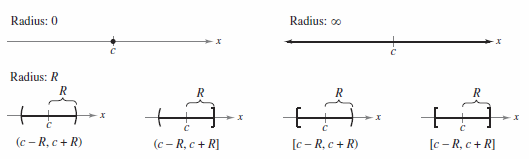
The number \(R\) is the convergence radius for the power series. If the series converges only at \(c\), then the convergence radius is \(R=0\). If the series converges for all \(x\), then the convergence radius is \(R=\infty\). All \(x\) values for which the power series converges is the power series' convergence interval.

Example 9.8.2 Finding the Convergence Radius for \(n!\) with the Ratio Test

Find the convergence radius for

$$ \sum_{n=0}^{\infty} n!x^{n}. $$

Solution Setting \(x=0\) yields

$$ f(0)= \sum_{n=0}^{\infty} n!0^{n} = 1+ 0 + 0 + \cdots = 1 $$

Any fixed value for \(x\) such that \(|x|>0\), let \(u_{n}=n!x^{n}\). Then

$$ \lim_{n \to \infty} \left | \frac{u_{n+1}}{u_{n}} \right|$$	$$= \lim_{n \to \infty} \left | \frac{(n+1)!x^{n+1}}{n!x^{n}} \right|$$
	$$=|x|\lim_{n \to \infty}(n+1)$$
	$$= \infty.$$

By the Ratio Test, the series diverges for \(|x| >0\) and converges only at its center, 0. The convergence radius is \(R=0\).

Example 9.8.3 Finding the Convergence Radius a constant multiplier with the Ratio Test

Find the convergence radius for

$$ \sum_{n=0}^{\infty} 3(x-2)^{n}. $$

Solution For \(x \ne 2\), let \(u_{n}=3(x-2)^{n}\). Then

$$ \lim_{n \to \infty} \left | \frac{u_{n+1}}{u_{n}} \right|$$	$$= \lim_{n \to \infty} \left | \frac{3(x-2)^{n+1}}{3(x-2)^{n}} \right|$$
	$$=\lim_{n \to \infty}|x-2|$$
	$$=|x-2|.$$

By the Ratio Test, the series converges for \(|x-2|< 1\) and diverges for \(|x-2| > 1\). The convergence radius is \(R=1\).

Example 9.8.4 Finding the Convergence Radius for an alternating series with the Ratio Test

Find the convergence radius for

$$ \sum_{n=0}^{\infty} \frac{(-1)^{n}x^{2n+1}}{(2n+1)!}. $$

Solution Let \(u_{n}= (-1)^{n}x^{2n+1}/(2n+1)!\). Then

$$ \lim_{n \to \infty} \left | \frac{u_{n+1}}{u_{n}} \right|$$	$$= \lim_{n \to \infty} \left |\frac{\frac{(-1)^{n+1}x^{2n+3}}{(2n+3)!}}{\frac{(-1)^{n}x^{2n+1}}{(2n+1)!}} \right|$$
	$$=\lim_{n \to \infty}\frac{x^{2}}{(2n+3)(2n+2)}.$$

Where \(x\) is any fixed value the limit is 0. By the Ratio Test, the series converges for all \(x\). The convergence radius is \(R=\infty\).

Endpoint Convergence

For a power series whose convergence radius is a finite number \(R\), Theorem 9.8.1 says nothing about the convergence at the endpoints for the convergence interval. Each endpoint must be tested separately for convergence or divergence. As a result, the convergence interval for a power series can take one among the six forms shown in Figure 9.8.2.

Convergence Intervals. Figure 9.8.2

Example 9.8.5 Find the Convergence Interval with Powers

Figure 9.8.3

Find the convergence interval for $$ \sum_{n=1}^{\infty} \frac{x^{n}}{n}. $$ Solution Let \(u_{n}=x^{n}/n\). Then $$ \lim_{n \to \infty} \left | \frac{u_{n+1}}{u_{n}} \right|$$ $$= \lim_{n \to \infty} \left |\frac{\frac{x^{n+1}}{(n+1)}}{\frac{x^{n}}{n}} \right|$$ $$=\lim_{n \to \infty} \left | \frac{nx}{n+1} \right|$$ $$=|x|.$$ By the Ratio Test the convergence radius is \(R=1\). Because the series is centered at 0, it converges in the interval (-1,1). This interval may not be the convergence interval. To determine that test for convergence at each endpoint. When \(x=1\) a divergent harmonic series $$ \sum_{n=1}^{\infty} \frac{1}{n} = \frac{1}{1} + \frac{1}{2} +\frac{1}{3}+\cdots \:\:\:\: \color{red}{\text{Diverges when }x=1.}$$ is produced. When \(x=-1\) a convergent alternating harmonic series $$ \sum_{n=1}^{\infty} \frac{(-1)^{n}}{n} = -1 + \frac{1}{2} -\frac{1}{3}+ \frac{1}{4} -\cdots \:\:\:\: \color{red}{\text{Converges when }x=-1.}$$ is produced. The convergence interval is [-1,1), as shown in Figure 9.8.3.

Example 9.8.6 Find the Convergence Interval and Endpoints with an Alternating Series

Figure 9.8.4

Find the convergence interval for $$ \sum_{n=1}^{\infty} \frac{(-1)^{n}(x+1)^{n}}{2^{n}}. $$ Solution Let \(u_{n}=(-1)^{n}(x+1)^{n}/2^{n} \). Then $$ \lim_{n \to \infty} \left | \frac{u_{n+1}}{u_{n}} \right|$$ $$= \lim_{n \to \infty} \left |\frac{\frac{(-1)^{n+1}(x+1)^{n+1}}{2^{n+1}}}{\frac{(-1)^{n}(x+1)^{n}}{2^{n}}} \right|$$ $$=\lim_{n \to \infty} \left | \frac{2^{n}(x+1}{2^{n+1}} \right|$$ $$=\left | \frac{x+1}{2} \right |.$$ By the Ratio Test the series converges for $$=\left | \frac{x+1}{2} \right | < 1 \text{ or } |x+1| < 2 .$$ This makes the convergence radius \(R=2\). Because the series is centered at \(x=-1\), it converges in the interval (-3,1). Testing the endpoints produces $$ \sum_{n=1}^{\infty} \frac{(-1)^{n}(-2)^{n}}{2^{n}} = \sum_{n=1}^{\infty}\frac{2^{n}}{2^{n}}=\sum_{n=1}^{\infty} 1 \:\:\:\: \color{red}{\text{Diverges when }x=-3.}$$ and $$ \sum_{n=1}^{\infty} \frac{(-1)^{n}(2)^{n}}{2^{n}} = \sum_{n=1}^{\infty} (-1)^{n} \:\:\:\: \color{red}{\text{Diverges when }x=1.}$$ proving that both endpoints diverge. The convergence interval is (-3,1), as shown in Figure 9.8.4.

Example 9.8.7 Find the Convergence Interval

Find the convergence interval for

$$ \sum_{n=1}^{\infty} \frac{x^{n}}{n^{2}}. $$

Solution Let \(u_{n}=x^{n}/n^{2}\). Then

$$ \lim_{n \to \infty} \left | \frac{u_{n+1}}{u_{n}} \right|$$	$$= \lim_{n \to \infty} \left |\frac{\frac{x^{n+1}}{(n+1)^{2}}}{\frac{x^{n}}{n^{2}}} \right|$$
	$$=\lim_{n \to \infty} \left | \frac{n^{2}x}{(n+1)^{2}} \right|$$
	$$=|x|.$$

By the Ratio Test the convergence radius is \(R=1\). Because the series is centered at \(x=0\), it converges in the interval (-1,1). When \(x=1\) a convergent \(p\)-series is produced. When \(x=-1\) a convergent alternating series is produced.

$$ \sum_{n=1}^{\infty} \frac{1}{n^{2}} = \frac{1}{1^{2}} + \frac{1}{2^{2}} +\frac{1}{3^{2}}++ \frac{1}{4^{2}}+\cdots \:\:\:\: \color{red}{\text{Converges when }x=1.}$$

$$ \sum_{n=1}^{\infty} \frac{(-1)^{n}}{n^{2}} = -\frac{1}{1^{2}} + \frac{1}{2^{2}} -\frac{1}{3^{2}}+ \frac{1}{4^{2}} -\cdots \:\:\:\: \color{red}{\text{Converges when }x=-1.}$$

The convergence interval is [-1,1].

Differentiation and Integration for Power Series

Theorem 9.8.1 Properties for Functions Defined by Power Series

If the function

$$f(x) $$	$$= \sum_{n=0}^{\infty} a_{n}(x-c)^{n} $$
	$$= a_{0} + a_{1}(x-c) + a_{2}(x-c)^{2} + a_{3}(x-c)^{3} + \cdots $$

has a convergence radius \(R>0\), then, on the interval

$$ (c-R,c+R)$$

\(f\) is differentiable and continuous. The derivative and antiderivative for \(f\) have the form

$$1.\:f{}^{\prime}(x) $$	$$= \sum_{n=0}^{\infty} na_{n}(x-c)^{n-1} $$
	$$= a_{1} + 2a_{2}(x-c) + 3a_{3}(x-c)^{2} + \cdots $$
$$2.\:\int f(x)\:dx $$	$$= C + \sum_{n=0}^{\infty} a_{n} \frac{(x-c)^{n-1}}{n+1} $$
	$$= C+ a_{0}(x-c) + a_{1}\frac{(x-c)^{2}}{2} + a_{2}\frac{(x-c)^{3}}{3} + \cdots $$

The convergence radius' obtained by differentiating or integrating a power series is the same as the original power series. The convergence interval may differ depending whether the endpoints converge or diverge.

Example 9.8.8 Convergence Intervals for \(f(x)\), \(f{}^{\prime}(x)\), and \(\int f(x)\:dx\)

Figure 9.8.5

Consider the function $$ \sum_{n=1}^{\infty} \frac{x^{n}}{n} = x + \frac{x^{2}}{2} + \frac{x^{3}}{3} + \cdots $$ Find the convergence interval for the following a. \(\int f(x)\:dx\) b. \(f(x)\) c. \(f{}^{\prime}(x)\) Solution By Theorem 9.8.2 $$f{}^{\prime}(x) $$ $$= \sum_{n=1}^{\infty} x^{n-1} $$ $$= 1 + x + x^{2} + x^{3} + \cdots $$ and $$\int f(x)\:dx $$ $$= C + \sum_{n=1}^{\infty} \frac{x^{n-1}}{n(n+1)} $$ $$= C+ \frac{x^{2}}{1\cdot2} + \frac{x^{3}}{2\cdot3} +\frac{x^{4}}{3 \cdot 4} + \cdots. 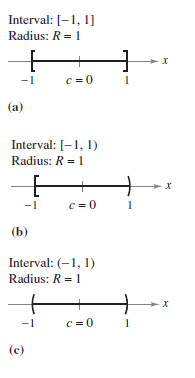$$ By the Ratio Test the convergence radius is \(R=1\). Considering the interval (-1,1) produces a. For \(\int f(x)\:dx\), the series $$ \sum_{n=1}^{\infty} \frac{x^{n-1}}{n(n+1)} \:\:\:\: \color{red}{\text{Convergence Interval: [-1,1]}}$$ converges for \(x= \pm 1\), and the convergence interval is [-1,1]. As shown in Figure 9.8.5(a). b. For \(f(x)\), the series $$ \sum_{n=1}^{\infty} \frac{x^{n}}{n} \:\:\:\: \color{red}{\text{Convergence Interval: [-1,1)}}$$ converges for \(x= -1\) and diverges for \(x=1\). The convergence interval is [-1,1). As shown in Figure 9.8.5(b). c. For \(f{}^{\prime}(x)\), the series $$ \sum_{n=1}^{\infty} x^{n-1} \:\:\:\: \color{red}{\text{Convergence Interval: (-1,1)}}$$ diverges for \(x= \pm 1\). The convergence interval is (-1,1). As shown in Figure 9.8.5(c). It appears that c. is the least likely to converge at the endpoints. In fact, it can be shown that if the series converges at the endpoints \(x=c \pm R\) then the series will also converge there.

Internal Links

Parent Article: Calculus II 09 Infinite Series