Calculus II 10.02 Plane Curves and Parametric Equations

Previous	Calculus II 10.01 Conics and Calculus
Next	Calculus II 10.03 Parametric Equations and Calculus

10.2 Plane Curves and Parametric Equations[1][2]

• Sketch the graph for a curve given by parametric equations.
• Eliminate the parameter in parametric equations.
• Find parametric equations to represent a curve.
• Understand the tautochrone and brachistochrone problems.

Plane Curves and Parametric Equations

Figure 10.2.1

Previously two-dimensional graphs were represented by a single equation with two variable. Parametric Equations use three variables in two equations to describe a curve on a plane. Consider a projectile's path through the air at a 45° angle with an initial 48 feet per second velocity. The projectile travels the parabolic path given by $$y=-\frac{x^{2}}{72}+x \:\:\:\: \color{red}{\text{Cartesian equation }} $$ as shown in Figure 10.2.1. This equation, however, does not take time into account. Introducing \(t\), called a parameter, produces the parametric equations \(x=24\sqrt{2}t \) \(\:\:\:\: \color{red}{\text{Parametric equation for }x} \) \(y=-16t^{2}+24\sqrt{2}t\) \( \:\:\:\: \color{red}{\text{Parametric equation for }y} \) By solving for \(t\) in seconds, at \(t=0\) the projectile starts at (0,0). At time \(t=1\) it is at \((24\sqrt{2},24\sqrt{2}-16)\) and so on. For this problem \(x\) and \(y\) are continuous functions for \(t\) and the resulting path is called a plane curve.

Definition 10.2.1 A Plane Curve

If \(f\) and \(g\) are continuous functions for \(t\) on an interval \(I\), then the equations

\(x=f(t)\) and \(y=g(t)\)

are parametric equations and \(t\) is the parameter. The point set \((x,y)\) obtained as \(t\) varies over \(I\) is the graph for the parametric equations. The parametric equations and the graph are a plane curve, denoted by \(C\).

Example 10.2.1 Sketching a Plane Curve with Time

Figure 10.2.2

When sketching a parametric equation curve on the \(xy\)-plane each point is based on the value for \(t\). Plotting the points as \(t\) increases produces a curve in time and space. This is called the curve's orientation. Sketch the curve described by the parametric equations below. \(x=f(t)=t^{2}-4\) and \(y=g(t)=\frac{t}{2}\) where \(-2 \leqslant t \leqslant 3\). Solution For integer values for \(t\) on the given interval yield the results in Table 10.2.1. Table 10.2.1 Integer values for \(t\) \(t\) -2 -1 0 1 2 3 \(x\) 0 -3 -4 -3 0 5 \(y\) -1 -1/2 0 1/2 1 3/2 The graph for curve \(C\) is shown in Figure 10.2.2. Notice the direction reverses at \(t=0\) from left to right and that \(x\) increases along with \(t\) as \(t\) increases from -2 to 3.

Figure 10.2.3

By the Vertical Line Test[3], curve \(C\) in Figure 10.2.2 does not define \(y\) as a function for \(x\). The advantage parametric equations over traditional functions is that they can describe graphs that are more general. The same graph can be described by two, or more, parametric equations. For example, the parametric equations $$x=4t^{2}-4 \text{ and } y=t, \text{ where } -1 \leqslant t \leqslant \frac{3}{2} $$ has the same graph as in Example 10.2.1. See Figure 10.2.3. Notice that \(t\) advances faster than in Example 10.2.1. In Figure 10.2.3 \(t\) reaches \((-3,-1/2)\) at \(t=-1/2\), twice as quickly at in Figure 10.2.2. Therefore, different parametric representations can represent various speeds at which objects travel along a given path.

Eliminating the Parameter

Finding a cartesian equation that represents the graph for parametric equations is called eliminating the parameter. In Example 10.2.1 arranging the equations as a simultaneous equations system[4], solving for \(t\) then back substituting produces the cartesian equation \(x=4y^{2}-4\), whose graph matches Figure 10.2.2.

The range for \(x\) and \(y\) in the parametric equations may be altered by changing the cartesian form. To maintain a match between the graphs adjust the parametric equations' domain accordingly. This is described in Example 10.2.2.

Example 10.2.2 Adjusting the Parametric Equations Domain

Figure 10.2.4

Sketch the curve represented by the equations $$ x=\frac{1}{\sqrt{t+1}} \text{ and } y=\frac{t}{t+1}, \:\: t > -1$$ by eliminating the parameter and adjusting the domain for the resulting cartesian equation. Solution Solving for \(t\) using simultaneous equations and adjusting the domain of the resulting cartesian equation. The cartesian equation, \(y=1-x^{2}\), is defined for all \(x\). But the parameter equation defines \(x\) only when \(t > -1\). This calls for restricting \(x\)'s domain to positive values as shown in Figure 10.2.4.

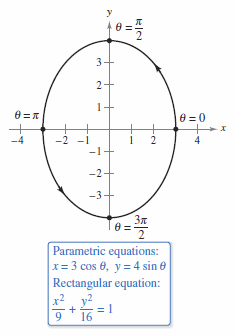
Example 10.2.3 Using Trigonometry to Eliminate a Parameter

Figure 10.2.5

Sketch the curve represented by the equations \( x=3 \cos \theta \text{ and } y=4 \sin \theta, \:\: 0 \leqslant \theta \leqslant 2 \pi\) by eliminating the parameter and finding the corresponding cartesian equation. Solution Begin by solving for \( \cos \theta \) and \(\sin \theta \). $$ \cos \theta =\frac{x}{3} \:\:\:\: \color{red}{\text{Solve for } \cos \theta} $$ $$ \sin \theta =\frac{y}{4} \:\:\:\: \color{red}{\text{Solve for } \sin \theta} $$ Use the identify \( \cos^{2} \theta + \sin^{2} \theta =1 \) to form an equation with only \(x\) and \(y\). \( \cos^{2} \theta + \sin^{2} \theta =1 \) Trigonometric identity $$\left ( \color{red}{\frac{x}{3}} \right )^{2} + \left ( \color{red}{\frac{y}{4}} \right )^{2} = 1 $$ Substitute $$ \frac{x^{2}}{9} + \frac{y^{2}}{16} = 1 $$ Cartesian Equation The graph is an ellipse centered at (0,0), with vertices at (0,4) and (0,-4), and the minor axis with length \(2b=6\), as shown in Figure 10.2.5. Not that the ellipse is traced out counterclockwise as \(\theta\) varies from 0 to \(2 \pi \). The graph for the parametric equations \( x=h + a \cos \theta \text{ and } y=k + b \sin \theta, \:\: 0 \leqslant \theta \leqslant 2 \pi\) is the counterclockwise ellipse given by $$ \frac{(x-h)^{2}}{a^{2}} + \frac{(y-k)^{2}}{b^{2}} = 1. $$ The graph for the parametric equations, notice \(\sin\) and \(\cos\) are reversed, \( x=h + a \sin \theta \text{ and } y=k + b \cos \theta, \:\: 0 \leqslant \theta \leqslant 2 \pi\) is the clockwise ellipse given by the same formula $$ \frac{(x-h)^{2}}{a^{2}} + \frac{(y-k)^{2}}{b^{2}} = 1. $$ The difference between counterclockwise and clockwise being where \(\sin\) and \(\cos\) are. Eliminating the parameter is primarily an aid to curve sketching. When the parametric equations represent the path for a moving object, the graph alone is not sufficient to describe the object’s motion. The parametric equations are needed to tell the position, direction, and speed at a given time.

Finding Parametric Equations

How can the parametric equations for a given graph or a given physical description be found? Since parametric representations are not unique, which one to choose? Example 10.2.4 finds two different parametric representations for a given graph.

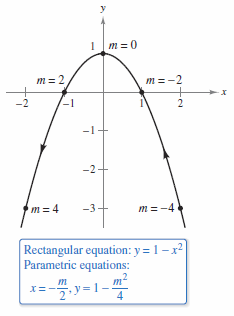
Example 10.2.4 Finding Parametric Equations for a Given Graph

Figure 10.2.6

Find a parametric equations that represents the graph for \(y=1-x^{2}\), using the following parameters. \(\textbf{a.}\: t=x\) $$\textbf{b.} \: \text{ The slope } m= \frac{dy}{dx} \:\text{ at the point } (x,y) $$ Solution a. Letting \(x=t\) produces the parametric equations \(x=t \text{ and } y=1-x^{2}=1-t^{2}\) b. Writing \(x\) and \(y\) as terms for \(m\) follows $$ m= \frac{dy}{dx} \:\:\:\:$$ $$ m= -2x \:\:\:\:$$ \( \color{red}{\text{Differentiate } y=1-x^{2}} \) $$ x= -\frac{m}{2} $$ \( \color{red}{\text{Solve for }x} \) This produces a parametric equation for \(x\). To obtain a parametric equation for \(y\) substitute \(-m/2\) for \(x\) in the original equation. \( y= 1-x^{2} \) \( \color{red}{\text{Original cartesian equation.}} \) $$ y=1 - \left( \color{red}{ -\frac{m}{2} } \right )^{2} \:\:\:\: $$ \( \color{red}{\text{Substitute}} \) $$ y= 1- \frac{m^{2}}{4} $$ \( \color{red}{\text{Simplify}} \) The parametric equations are $$x=-\frac{m}{2} \text{ and } y= 1- \frac{m^{2}}{4}. $$ In Figure 10.2.6, note that the resulting curve is drawn right-to-left as the slope \(m\) increases. For part (a), the curve has the opposite orientation.

Example 10.2.5 Parametric Equations for a Cycloid[5]

Determine the curve traced by a point \(P\) on a circle's circumference with radius \(a\) rolling along a straight line on a plane. Such a curve is called a cycloid.
Solution Let the parameter \(\theta\) measure the circle's rotation. Let \(P=(x,y)\) be the origin. When \(\theta=0, \:P\) is at the origin. When \(\theta=\pi,\: P\) is at a maximum point \((\pi a, 2a)\). When \(\theta=2\pi,\: P\) is back on the \(x\)-axis at \((2 \pi a,0)\). Figure 10.2.7 shows that \( \angle APC= 180^{\circ}-\theta\). Therefore,

$$ \sin \theta = \sin (180^{\circ}-\theta) = \sin (\angle APC) = \frac{AC}{a}=\frac{BD}{a} $$

$$ \cos \theta = -\cos (180^{\circ}-\theta) = -\cos (\angle APC) = \frac{AP}{-a} $$

which implies that \(AP=-a \cos \theta\) and \(BD= a \sin \theta\).

Because the circle rolls along the \(x\)-axis, \(OD=\widehat{PD}= a \theta\) and \(BA=DC=a\). Therefore,

\(x=OD-BD= a \theta- a \sin \theta\)

\(y=BA+AP=a - a \cos \theta\).

The parametric equations are

\(x=a( \theta- \sin \theta)\) and \(y=a(1 - \cos \theta)\).

Figure 10.2.7

Definition 10.2.2 Smooth Curve

A curve \(C\) represented by \(x=f(t)\) and \(y=g(t)\) on an interval \(I\) is called smooth when \(f{}^{\prime}\) and \(g{}^{\prime}\) are continuous on \(I\) and not simultaneously 0, except possibly at \(I\)'s endpoints. The curve \(C\) is called piecewise smooth when it is smooth on each subinterval over \(I\).

The cycloid in Figure 10.2.7 has sharp corners at the values \(x=2n\pi a\). Notice that the derivatives \(x{}^{\prime}(\theta)\) and \(y{}^{\prime}(\theta)\) are both zero at the points where \(\theta=2n\pi\).

\(x(\theta)=a( \theta- \sin \theta) \)	\(y(\theta)=a(1 - \cos \theta)\)
\(x{}^{\prime}(\theta)= a-a \cos \theta \)	\(y{}^{\prime}(\theta)= a \sin \theta \)
\(x{}^{\prime}(2n\pi)= 0 \)	\(y{}^{\prime}(2n \pi)= 0 \)

Between these points the cycloid is called smooth. The cycloid is piecewise smooth over the interval.

The Tautochrone[6] and Brachistochrone[7] Problems

Figure 10.2.8 Figure 10.2.9 Figure 10.2.10

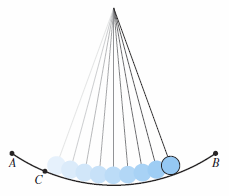
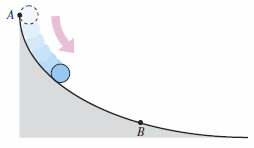
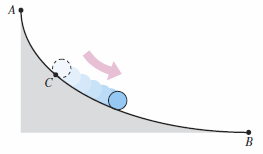
The curve described in Example 10.2.5 is related to The Tautochrone Problem. Galileo[8] discovered the time required for a pendulum to complete a full swing is approximately the same whether it makes a large movement at high speed or a small movement at lower speed as shown in Figure 10.2.8. Later Galileo realized that he could use this principle to construct a clock but the mechanics were unsolvable at the time. Time would wait for Christian Huygens[9] (1629–1695) to design and construct the first working pendulum clock. While working on pendulums Huygens realized that a pendulum does not take exactly the same time to complete swings with varying lengths. To correct this he gave the swinging pendulum a slight boost each time it passes the lowest point. But Huygens discovered that a ball rolling back and forth on an inverted cycloid does complete each cycle in exactly the same time. John Bernoulli[10] in 1696 proposed the Brachistochrone problem—in Greek, brachys means short and chronos means time. The problem was to determine the path down which a particle (such as a ball) will slide from point \(A\) to point \(B\) in the shortest time. Several mathematicians took up the challenge, and the following year the problem was solved by Newton, Leibniz, L’Hôpital, John Bernoulli, and James Bernoulli. As it turns out, the solution is not a straight line from \(A\) to \(B\) but an inverted cycloid passing through the points \(A\) and \(B\) as shown in Figure 10.2.9 The amazing part to the Brachistochrone problem is that a particle starting at rest at any point \(C\) on the cycloid between \(A\) and \(B\) will take exactly the same time to reach \(B\), as shown in Figure 10.2.10.

Internal Links

Parent Article: Calculus II 10 Conics Parametric Equations and Polar Coordinates