Calculus I 02.06 Related Rates

Previous	Calculus I 02.05 Implicit Differentiation
Next	Calculus I 03 Differentiation Applications

2.6 Related Rates

Volume is related to radius and height. Figure 2.6.1

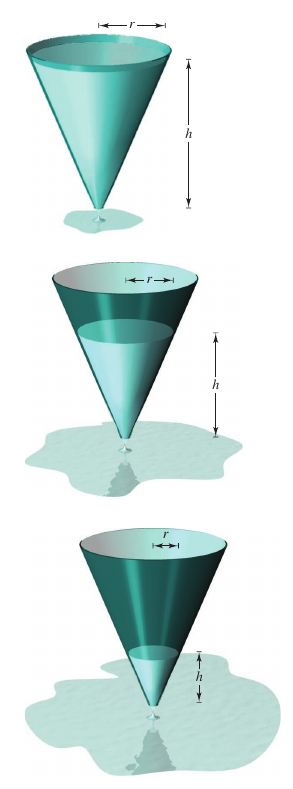
Find a related rate. Use related rates to solve real-life problems. Finding Related Rates The Chain Rule is used to find the change rates between two or more related variables that are change with respect to time. For example, when water is drained from a conical tank, as shown in Figure 2.6.1, the volume \(V\), the radius \(r\), and the height \(h\) for the water level are all functions in time \(t\). These variables are related by the equation $$V=\frac{\pi}{3}r^2h$$     Original Equation differentiate implicitly with respect to \(t\) to produce the related-rate equation $$\frac{d}{dt}[V]$$ $$=\frac{d}{dt} \left [ \frac{\pi}{3}r^2h \right ]$$ $$\frac{dV}{dt}$$ $$=\frac{\pi}{3} \left [ r^2 \frac{dh}{dt}+h\left ( 2r\frac{dr}{dt} \right ) \right ]$$     Differentiate with respect to \(t\). $$= \frac{\pi}{3} \left ( r^2 \frac{dh}{dt} + 2rh\frac{dr}{dt} \right ).$$ This demonstrates the change rate for \(V\) is related to the change rates for both \(h\) and \(r\).

Example 2.6.1 Two Related Rates

The variables \(x\) and \(y\) are both differentiable functions for \(t\) and are related by the equation

\(y=x^2+3.\)

Find \(dy/dt\) when \(x=1\), given that \(dx/dt=2\) when \(x=1\).
Solution Apply the Chain Rule to differentiate both sides with respect to \(t\).

\(y\)	\(=x^2+3\)	Original equation
$$\frac{d}{dt}[y]$$	$$=\frac{d}{dt}[x^2+3]$$	Differentiate with respect to \(t\).
$$\frac{dy}{dt}$$	$$=2x\frac{dx}{dt}$$	Chain Rule

When \(x=1\) and \(dx/dt=2\) the equation solves to

$$\frac{dy}{dt}=2(1)(2)=4.$$

Problem Solving with Related Rates

In Example 2.6.1 the equation relating the variables and the change rate with respect to \(t\) was given.

Equation:	\(y=x^2+3\)
Given rate:	$$\frac{dx}{dt}=2$$	when \(x=1\)
Find:	$$\frac{dy}{dt}$$	when \(x=1\)

The following exercises leave creating the mathematical model to the student.

Example 2.6.2 Ripples in a Pond

Total area increases as the outer radius increases. Figure 2.6.2

A pebble is dropped into a calm pond causing ripples to radiate from the drop point in concentric circles, as shown in Figure 2.6.1. The outer ripple's radius \(r\) is increasing at a constant rate at 1 foot per second. When the radius is 4 feet, at what rate is the total rippled area \(A\) changing? Solution The variables \(r\) and \(A\) are related by \(A=\pi r^2\). The area for a circle. The change rate for the radius \(r\) is \(dr/dt=1\). Equation: \(A=\pi r^2\) Given rate: $$\frac{dr}{dt}=1$$ Find: $$\frac{dA}{dt}$$ when \(r=4\) Proceed as in Example 2.6.1. $$\frac{d}{dt}[A]$$ $$=\frac{d}{dt}[\pi r^2]$$     Differentiate with respect to \(t\). $$\frac{dA}{dt}$$ $$=2 \pi r \frac{dr}{dt}$$     Chain Rule \(=2 \pi (\color{red}{4})(\color{red}{1})\)     Substitute 4 for \(r\) and 1 for \(\frac{dr}{dt}\). \(=8 \pi\) square feet per second     Simplify. When the radius is 4 feet the change rate for the area is \(8 \pi\) square feet per second.

Guidelines for Solving Related-Rate Problems

1.	Identify all given and undetermined quantities. Make a sketch and label the quantities.
2.	Write an equation involving the variables whose change rates either are given or unknown.
3.	Apply the Chain Rule and implicitly differentiate both sides with respect to time \(t\). Only then go onto Step 4 below.
4.	Next, substitute into the resulting equation all known values for the variables and their change rates. Then solve for the required change rate.

Table 2.6.1 below lists mathematical models for change rates. For example, the change rate in the first example is a car's velocity.

Table 2.6.1 Change Rates
Verbal Statement	Mathematical Model
A car's velocity after traveling for 1 hour at 50 miles per hour.	\(x=\) distance traveled $$\frac{dx}{dt}=50 \text{ mi/h when }t=1$$
Water filling a swimming pool at a 10 cubic meter per hour rate.	\(V=\) water volume in pool $$\frac{dV}{dt}=10 m^3/h$$
A gear is revolving with a 25 revolutions per minute rate. One revolution \(=25 \pi\) rad.	$$\frac{d \theta}{dt} = 25(2 \pi) \text{ rad/min}$$ \(\theta = \) revolution angle
A bacteria colony is increasing at a 2000 per hour rate.	\(x=\) colony size $$\frac{dx}{d}=2000 \text{ bacteria per hour}$$

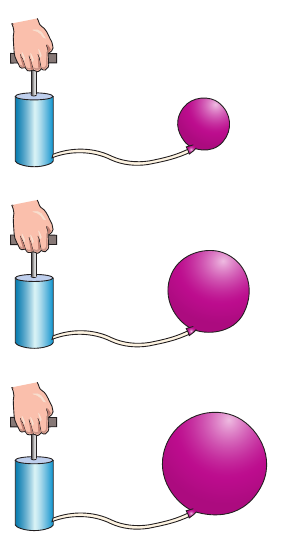
Example 2.6.3 An Inflating Balloon

Inflating a balloon Figure 2.6.3

Air is being pumped into a spherical balloon, as shown in Figure 2.6.3, at a 4.5 cubic foot per minute rate. Find the change rate for the radius when it reaches 2 feet. Solution Let \(V\) be the balloon's volume and let \(r\) be its radius. Because the volume is increasing at a 4.5 cubic feet per minute rate, that at time \(t\) the change rate for the volume is \(dV/dt=9/2\). The problem breaks down as shown. Given rate: $$\frac{dV}{dt}=\frac{9}{2} \text{ (constant rate)}$$ Find: $$\frac{dr}{dt} \text{ when }r=2$$ To find the change rate for the radius produce an equation that relates the radius \(r\) to the volume \(V\). Equation: $$V=\frac{4}{3} \pi r^3$$     Sphere volume Differentiating both sides with respect to \(t\) produces $$\frac{dV}{dt}=4\pi r^2 \frac{dr}{dt}$$     Differentiate with respect to \(t\). $$\frac{dr}{dt}= \frac{1}{4 \pi(2)^2} \left ( \frac{dV}{dt} \right ).$$     Solve for \(dr/dt\). When \(r=2\), the change rate for the radius is $$\frac{dr}{dt}=\frac{1}{4 \pi(2)^2} \left ( \frac{9}{2} \right ) \approx 0.09 \text{ foot per minute}$$

In Example 2.6.3, note that the volume is increasing at a constant rate, but the radius is increasing at a variable rate. When two, or more, rates are related it does not mean they are equal or proportional. In this particular case, the radius is growing more, and more slowly, as \(t\) increases.

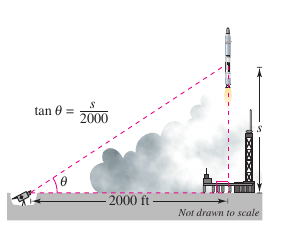
Example 2.6.4 An Airplane's Speed as Tracked by Radar

An airplane is flying at 6 miles high and \(s\) miles from the radar. Figure 2.6.4

An airplane is flying on a flight path that will take it directly over a radar tracking station, as shown in Figure 2.6.4. The distance \(s\) is decreasing at a 400 miles per hour rate when \(s=10\) miles. What is the plane's speed? Solution Let \(x\) be the horizontal distance from the radar, as shown in Figure 2.6.4. Notice that when \(s=10\), \(x=\sqrt{10^2-36}=8\). Given rate: \(ds/dt=-400\) when \(s=10\) Find: \(dx/dt\) when \(s=10\) and \(x=8\) Find the plane's velocity as shown. Equation: \(x^2+6^2\) \(=s^2\)     Pythagorean Theroem $$2x\frac{dx}{dt}$$ $$=2s \frac{ds}{dt}$$     Differentiate with respect to \(t\). $$\frac{dx}{dt}$$ $$=\frac{s}{x} \left ( \frac{ds}{dt} \right )$$     Solve for \(dx/dt\). $$= \frac{\color{red}{10}}{\color{red}{8}} (\color{red}{-400})$$     Substitute for \(s,\:x,\:ds/dt\). \(=-500\) miles per hour     Simplify. Because the velocity is -500 miles per hour, the speed is 500 miles per hour. This is negative because it represents a distance that is decreasing.

Example 2.6.5 A Changing Elevation Angle

The rocket rises vertically by, \(s=50t^2\), where \(s\) is feet and \(t\) is seconds. The TV camera is 2000 feet from the launch pad. Figure 2.6.5

Find the change rate in the elevation angle for the TV camera in Figure 2.6.5 at 10 seconds after lift-off. Solution Let \(\theta\) be the elevation angle, as shown in Figure 2.6.5. When \(t=10\), the rocket's height is \(s\) where \(s=50t^2=50(\color{red}{10})^2=5000\) feet. Given rate: \(ds/dt=100t=\) rocket velocity Find: \(d\theta/dt\) when \(t=10\) and \(s=5000\) Use Figure 2.6.5 to relate \(s\) and \(\theta\) by the equation \(\tan \theta=s/2000.\) When \(t=10\) and \(s=5000\), the equation produces $$\frac{d\theta}{dt}=\frac{2000(100)(10)}{5000^2+2000^2}=\frac{2}{29} \text{ radians per second. }$$ When \(t=10\) , \(\theta\) the change rate is \(2/29\) radians per second.

Example 2.6.5 A Changing Elevation Angle

Law of Cosines: \(b^2=a^2+c^2-2ac \cos \theta\). Figure 2.6.6

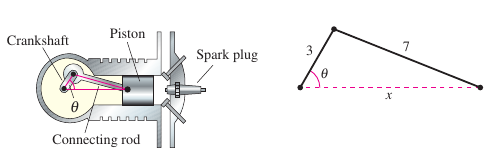
In Figure 2.6.7, a 7-inch connecting rod is fastened to a crank with a 3 inch radius. The crankshaft rotates counterclockwise at a constant 200 revolutions per minute rate. Find the piston's velocity when \(\theta =\pi/3\). The piston velocity is related to the crankshaft angle. Figure 2.6.7 Solution Label the distances as shown in Figure 2.6.6. Because a complete revolution corresponds to \(2\pi\) radians, it follows that \(d\theta/dt=200(2\pi)=400 \pi\) radians per minute. Given rate: $$\frac{d\theta}{dt}=400 \pi \text{ (constant rate)}$$ Find: $$\frac{dx}{dt} \text{ when } \theta=\frac{\pi}{3}$$ Apply the Law of Cosines, as shown in Figure 2.6.6 to find an equation that relates to \(x\) and \(\theta\). Therefore, when \(x=8\) and \(\theta=\pi/3\), the piston velocity is $$\frac{dx}{dt}$$ $$=\frac{6(8)(\sqrt{3}/2)}{6(1/2)-16}(400\pi)$$ $$=\frac{9600\pi\sqrt{3}}{-13}$$ \(\approx -4018\) inches per minute.

Internal Links

Parent Article: Calculus I 02 Differentiation