Calculus I 03.04 Concavity and the Second Derivative Test
| Previous | Calculus I 03.03 Increasing and Decreasing Functions and the First Derivative Test |
| Next | Calculus I 03.05 Limits at Infinity |
Contents
3.4 Concavity and the Second Derivative Test
- Determine intervals on which a function is concave upward or concave downward.
- Find any inflection points on the graph for a function.
- Apply the Second Derivative Test to find relative extrema for a function.
Concavity
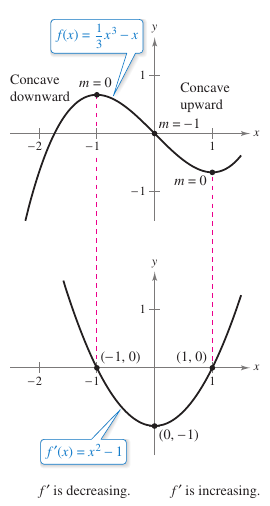
Locating the intervals where \({f}'\) increases or decreases can be used to determine where the graph for \(f\) is curving upward or curving downward.
|
|
Definition 3.4.1 ConcavityLet \(f\) be differentiable on an open interval \(I\). The graph for \(f\) is concave upward on \(I\) when \({f}'\) is increasing on the interval and concave downward on \(I\) when \({f}'\) is decreasing on the interval.
|
Theorem 3.4.1 shows how to use the second derivative for a function \(f\) to determine intervals on which the graph for \(f\) is concave upward or downward. The proof follows directly from Theorem 3.3.1 and the concavity definition.
Theorem 3.4.1 Test for Concavity
Let \(f\) be a function whose second derivative exists on an open interval \(I\).
1. If \({f}(x)>0 for all \(x\) in \(I\), then the graph for \(f\) is concave upward on \(I\).
2. If \({f}(x)<0 for all \(x\) in \(I\), then the graph for \(f\) is concave downward on \(I\).
3. If \({f}(x)=0 for all \(x\) in \(I\), then the graph for \(f\) is not concave on \(I\).
To apply Theorem 3.4.1, locate the \(x\)-values at which \({f}''(x)=0\) or \({f}''\) does not exist. Use these \(x\)-values to determine the test intervals. Finally, test the sign for \({f}''(x)\) in each test intervals.
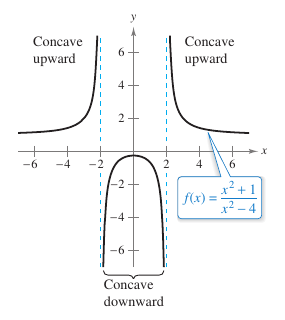
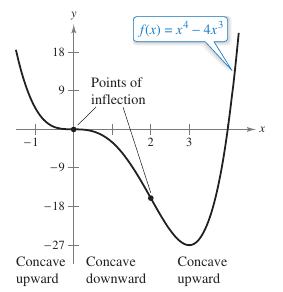
Example 3.4.1 Determining Concavity
|
|
Determine the open intervals on which the graph for
is concave upward or downward.
Because \({f}''=0\) when \(x= \pm 1\) and \({f}''\) is defined on the entire real number line. Test \({f}''\) on the intervals \((-\infty,-1)\), \((-1,1)\), and \((1,\infty)\). The results are shown in Table 3.4.1 and in Figure 3.4.3.
| |||||||||||||||||||||||||||||||||||
The function given in Example 3.4.1 is continuous on the entire real number line. When there are \(x\)-values at which the function is not continuous, these values should be used, along with the points at which \({f}''(x)=0\) or \({f}''(x)\) does not exist, to form the test intervals
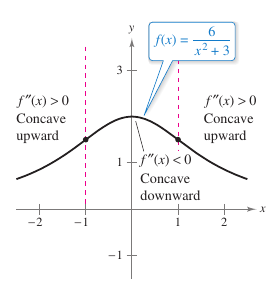
Example 3.4.2 Determining Concavity
|
|
Determine the open intervals on which the graph for
is concave upward or downward.
There are no points at which \({f}''(x)=0\), but at \(x=\pm 2\), the function \(f\) is not continuous. Test for concavity in the intervals \((-\infty,-2)\), \((-2,2)\), and \((2,\infty)\) as shown in Table 3.4.2. The graph for \(f\) is shown in Figure 3.4.4.
| |||||||||||||||||||||||||||||||||||
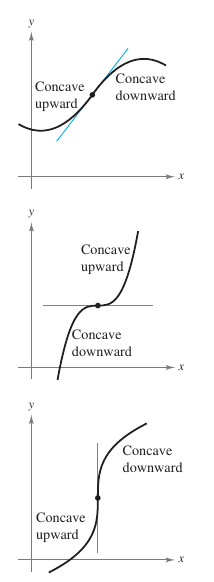
Inflection Point
|
|
The graph in Figure 3.4.3 has two points where the concavity changes. If the tangent line to the graph exists at such a point, then that point is an inflection point. Figure 3.4.5 shown inflection points in three types. Definition 3.4.2 Inflection PointLet \(f\) be a continuous function on an open interval. Let \(c\) be a point in that interval. If the graph for \(f\) has a tangent line at this point \((c,f(c))\), then this point is an inflection point. This point is where the concavity changes from upward to downward or the reverse. Some sources use a definition that does not require a tangent line at the inflection point. For example, the function
does not have an inflection point at the origin, even though the concavity for the graph changes from downward to upward. To locate possible inflection points determine the \(x\)-values for which \({f}''(x)=0 \text{ or } {f}''(x)\) does not exist. This is similar to locating extrema for \(f\). Theorem 3.4.2. Inflection PointIf \((c,f(c))\) is and inflection point on the graph for \(f\), then either \({f}''(c)=0\) or \({f}''\) does not exist at \(x=c\).
Example 3.4.3 Finding Inflection PointsDetermine the inflection points and discuss the concavity for the graph for
Solution Differentiating twice produces the following.
Solving \({f}''(x)=0\) produces possible inflection points at \(x=0\) and \(x=2\). Testing the intervals between these \(x\)-values determines they both yield inflection points.The testing is shown below in Table 3.4.3. The graph for \(f\) is shown in Figure 3.4.6.
| ||||||||||||||||||||||||||||
|
|
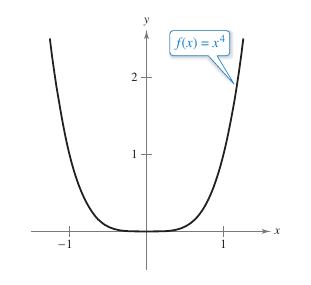
The converse for Theorem 3.4.2 is not generally true. It is possible for the second derivative to equal zero at a point that is not an inflection point. For example, the graph for \(f(x)=x^4\) is shown in Figure 3.4.7. The second derivative is zero when \(x=0\), but the point \((0,0)\) is not an inflection point because the graph is concave upward in both intervals \(-\infty < x < 0\) and \(0<x<\infty\). |
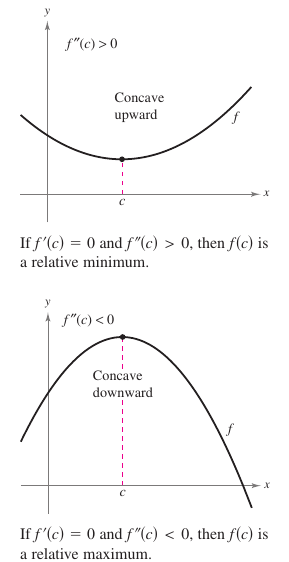
The Second Derivative Test
|
|
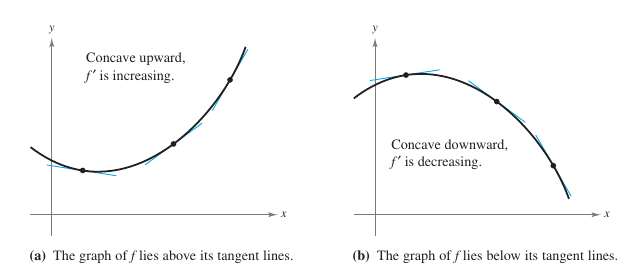
The second derivative is used to test for concavity and for relative extrema. If the graph for a differentiable function \(f\) is concave upward on an open interval containing \(c\), and \({f}'(c)=0\), then \(f(c)\) must be a relative minimum for \(f\). Conversely, if the graph for a differentiable function \(f\) is concave downward on an open interval containing \(c\), and \({f}'(c)=0\), then \(f(c)\) must be a relative maximum for \(f\),as shown in Figure 3.4.8. This is defined in Theorem 3.4.3. Theorem 3.4.3 Second Derivative TestLet \(f\) be a differential function such that \({f}'(c)=0\) and the second derivative for \(f\) exists on an open interval containing \(c\).
for all \(x \neq c\) in \(I\). If \(x<c\), then \(x-c<0\) and \({f}'(x)<0\). If \(x>c\), then \(x-c>0\) and \({f}'(x)>0\). Therefore, \({f}'(x)\) changes from negative to positive at \(c\), and the First Derivative Test implies that \(f(c)\) is a relative minimum. The second case is proven in the same manner. |
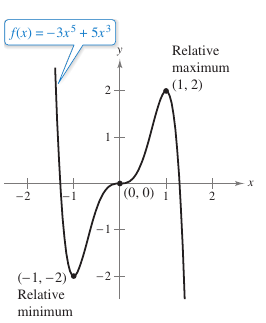
Example 3.4.4 Using the Second Derivative Test
|
|
Find the relative extrema for
Solution Begin by finding the first derivative for \(f\).
The first derivative yields \(x=-1,\:0, \text{ and }1\) are the only critical numbers for \(f\). By finding the second derivative
the Second Derivative Test can be applied as shown in Table 3.4.4 below.
Because the Second Derivative Test fails at \((0,0)\), the First Derivative Test yields that \(f\) increases to the left and right fpr \(x=0\). Therefore, \((0,0)\) is neither a relative minimum nor a relative maximum even though the graph has a horizontal tangent line at this point. The graph for \(f\) is shown in Figure 3.4.9. | ||||||||||||||||
Internal Links
Parent Article: Calculus I 03 Differentiation Applications