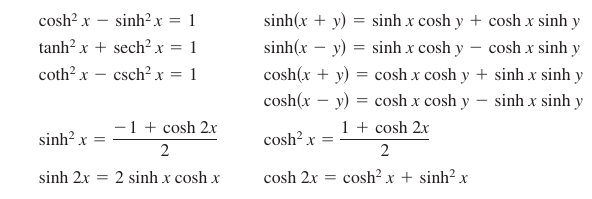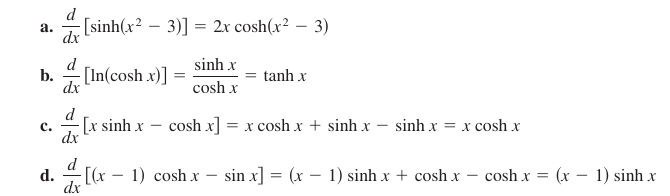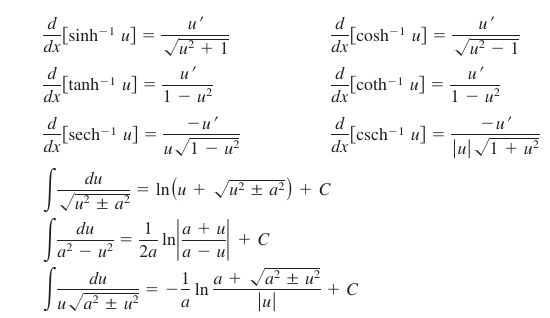Calculus I 05.08 Hyperbolic Functions

Previous	Calculus I 05.07 Inverse Trigonometric Functions: Integration
Next	Calculus II

5.8 Hyperbolic Functions

• Hyperbolic function properties.
• Differentiate and integrate hyperbolic functions.
• Inverse hyperbolic functions properties.
• Differentiate and integrate functions involving inverse hyperbolic functions.

Hyperbolic Functions

Hyperbolic functions are special exponential functions first described in detail by Johann Heinrich Lambert[1]. The term hyperbolic function arose by comparing the area for a semicircular region with the area for the region under a hyperbola, as shown in Figure 5.8.1.

Note the semicircle and hyperbola have the same width.
Figure 5.8.1

The integral for the semicircular region involves an inverse trigonometric, circular, function:

$$\int_{-1}^{1} \sqrt{1-x^2}\:dx= \frac{1}{2} \left [\vphantom{ \frac{3}{4} } x\sqrt{1-x^2} \arcsin x \right ]_{-1}^{1}=\frac{\pi}{2} \approx 1.571.$$

The integral for the hyperbolic region involves an inverse hyperbolic function:

$$\int_{-1}^{1} \sqrt{1-x^2}\:dx= \frac{1}{2} \left [\vphantom{ \frac{3}{4} } x\sqrt{1-x^2} \sinh^{-1} x \right ]_{-1}^{1}=\frac{\pi}{2} \approx 2.296.$$

Hyperbolic functions are similar to trigonometric functions in many ways.

Definition 5.8.1 Hyperbolic Functions

$$\sinh x = \frac{e^x-e^{-x}}{2}$$	$$\operatorname{csch} x = \frac{1}{\sinh x}, \: x \ne 0$$
$$\cosh x = \frac{e^x+e^{-x}}{2}$$	$$\operatorname{sech} x = \frac{1}{\cosh x}$$
$$\tanh x = \frac{\sinh x}{\cosh x}$$	$$\coth x = \frac{1}{\tanh x},\: x \ne 0$$

The notation \(\sinh x\) is read as “the hyperbolic sine for x,” \(\cosh x\) as “the hyperbolic cosine of x,” and so on.

The graphs for the six hyperbolic functions, domains and ranges are shown in Figure 5.8.1 below. Note the graph for \(\sinh x\) can be obtained by adding the corresponding \(y\)-coordinates for the exponential functions \(f(x)=\frac{1}{2}e^x\) and \(g(x)=-\frac{1}{2}e^{-x}\). Likewise, the graph for \(\cosh x\) can be obtained by adding the corresponding \(y\)-coordinates for the exponential functions \(f(x)=\frac{1}{2}e^x\) and \(h(x)=\frac{1}{2}e^{-x}\).

Figure 5.8.2

Many trigonometric identities have corresponding hyperbolic identities. For instance,

$$\cosh^2 x- \sinh^2 x$$	$$=\left ( \frac{e^x+e^{-x}}{2} \right )^2-\left ( \frac{e^x-e^{-x}}{2} \right )^2$$
	$$=\frac{e^{2x}+2+e^{-2x}}{4}-\frac{e^{2x}-2+e^{-2x}}{4}$$
	$$=\frac{4}{4}$$
	\(=1.\)

Hyperbolic Identities

Hyperbolic Differentiation and Integration

Because the hyperbolic functions are written in the form \(e^x\) and \(e^{-x}\), deriving the rules for their derivatives is easy. Theorem 5.8.1 lists these derivatives with the corresponding integration rules.

Theorem 5.8.1 Hyperbolic Derivatives and Integrals

Let \(u\) be a differentiable function for \(x\).

Proof Here is a proof for two differentiation rules. The others are left as an exercise.

$$\frac{d}{dx} \left [ \sinh x \right ]$$	$$=\frac{d}{dx} \left [ \frac{e^x-e^{-x}}{2} \right ]$$
	$$=\frac{e^x+e^{-x}}{2} $$
	\(=\cosh x\)
$$\frac{d}{dx} \left [ \tanh x \right ]$$	$$=\frac{d}{dx} \left [ \frac{\sinh x }{\cosh x} \right ]$$
	$$=\frac{ \cosh x (\cosh x) - \sinh x (\sinh x)}{\cosh^2 x}$$
	$$=\frac{1}{\cosh^2 x}$$
	\(=\operatorname{sech}^2 x\)

Example 5.8.1 Hyperbolic Function Differentiation

Example 5.8.2 Finding Relative Extrema

Figure 5.8.3

Find the relative extrema for \(f(x)=(x-1) \cosh x - \sinh x.\) Solution Using the result from Example 5.8.1(d), set the first derivative for \(f\) equal to 0. \((x-1) \sinh x = 0\) The critical numbers are \(x=1\) and \(x=0\). Using the Second Derivative Test, verify the point \((0,-1)\) yields a relative maximum and the point \((1, -\sinh 1)\) yields a relative minimum, as shown in Figure 5.8.3. Try using a graphing program to confirm this result. If your graphing utility does not have hyperbolic functions, you can use exponential functions, as shown. $$f(x)$$ $$=(x-1)\left ( \frac{1}{2} \right )\left ( e^x+e^{-x} \right )-\frac{1}{2}\left ( e^x-e^{-x} \right )$$ $$=\frac{1}{2} \left ( xe^x+xe^{-x}-e^x-e^{-x}-e^x+e^{-x} \right )$$ $$= \frac{1}{2}\left ( xe^x+xe^{-x}-2e^x \right )$$

Example 5.8.3 Hanging Power Cables

Catenary Figure 5.8.4

When a uniform flexible cable, such as a telephone wire, is suspended from two points, it forms a shape called a catenary[2]. Power cables are suspended between two towers, forming a catenary shown in Figure 5.8.4. The equation for this catenary is $$y=a \cosh \frac{x}{a}.$$ The distance between the two towers is \(2b\). Find the slope for the catenary at the point where the cable meets the right-hand tower. Solution Differentiation produces $${y}'=a \left ( \frac{1}{a} \right ) \sinh \frac{x}{a}=\sinh \frac{x}{a}.$$ At the point \((b, a \cosh (b/a))\), the slope, from the left, is \(m=\sinh\frac{b}{a}.\)

Example 5.8.4 Integrating a Hyperbolic Function

Find

$$\int \cosh 2x \sinh^2 2x\:dx.$$

Solution

$$\int \cosh 2x \sinh^2 2x\:dx$$	$$=\frac{1}{2} \int \left ( \sinh 2x \right )^2 \left ( 2 \cosh 2x \right )\:dx$$	\(u=\sinh 2x\)
	$$= \frac{1}{2} \left [ \frac{\left ( \sinh 2x \right )^3 }{3} \right ] +C$$
	$$= \frac{ \sinh^3 2x}{6}+C$$

Inverse Hyperbolic Functions

Unlike trigonometric functions, hyperbolic functions are not periodic. Consider Figure 5.8.2, four hyperbolic functions are actually one-to-one. The hyperbolic sine, tangent, cosecant, and cotangent. Applying Theorem 5.3.2 concludes that these four functions have inverse functions. The other two functions, the hyperbolic cosine, and secant, are one-to-one when their domains are restricted to the positive real numbers, and for this restricted domain they also have inverse functions. Because the hyperbolic functions are defined in exponential forms, it is not surprising that the inverse hyperbolic functions can be written in logarithmic terms, as shown in Theorem 5.8.2 below.

Theorem 5.8.2 Inverse Hyperbolic Functions

Proof The exponential and logarithmic function properties applied in a straightforward manner will prove the theorem. For example, for

$$f(x)=\sinh x = \frac{e^x-e^{-x}}{2}$$

and

\(g(x)= \ln \left ( x + \sqrt{x^2+1} \right )\)

produces

\(f(g(x))=x\) and \(g(f(x))=x\)

which implies that \(g\) is the inverse function for \(f\).

Graphs for the hyperbolic tangent and inverse hyperbolic tangent functions Figure 5.8.5

A graphing program can confirm the results from Theorem 5.8.2. For instance, graph the following functions. The resulting display is shown in Figure 5.8.6. As the graphs are traced out, notice that \(y_1=y_2\) and \(y_3=y_4\). Also notice the graph for \(y_1\) reflects the graph for \(y_3\) along the line \(y=x\).

The graphs for the hyperbolic inverse functions are shown in Figure 5.8.6.

Figure 5.8.6

The inverse hyperbolic secant can define a curve called a tractrix or pursuit curve, as discussed in Example 5.8.5.

Example 5.8.5 A Tractrix

A person must walk about 41.27 feet to bring the boat to a position 5 feet from the dock. Figure 5.8.6

A person is holding a rope that is tied to a boat, as shown in Figure 5.8.6. As the person walks along the dock, the boat travels along a tractrix, given by the equation $$y= a \operatorname{sech}^{-1} \frac{x}{a} - \sqrt{a^2-x^2}$$ where \(a\) is the rope's length. For \(a=20\) feet, find the distance the person must walk to bring the boat to a position 5 feet from the dock. Solution In Figure 5.8.6, notice the distance the person has walked is \(y_1\) \(=y+\sqrt{20^2-x^2}\) $$=\left ( 20 \operatorname{sech}^{-1} \frac{x}{20} - \sqrt{20^2-x^2} \right ) + \sqrt{20^2-x^2}$$ $$=20 \operatorname{sech}^{-1} \frac{x}{20}.$$ When \(x=5\), this distance is $$y_1=20 \operatorname{sech}^{-1} \frac{5}{20} \ln \frac{1+\sqrt(1-(1/4)^2} = 20 \ln (4+\sqrt{15}) \approx 41.27\:\text{feet.}$$ The person must walk about 41.27 feet to bring the boat to a position 5 feet from the dock.

Inverse Hyperbolic Functions: Differentiation and Integration

The derivatives for the inverse hyperbolic functions, which resemble the derivatives for the inverse trigonometric functions, are listed in Theorem 5.8.3 with the corresponding integration formulas in logarithmic form. Verify each formula by applying the logarithmic definitions for inverse hyperbolic functions.

Theorem 5.8.3 Differentiation and Integration Involving Inverse Hyperbolic Functions

Let \(u\) be a differentiable function for \(x\).

Example 5.8.6 Inverse Hyperbolic Function Differentiation

a.	$$\frac{d}{dx} \left [ \sinh^{-1} (2x) \right ]$$	$$=\frac{2}{\sqrt{(2x)^2+1}}$$
		$$=\frac{2}{\sqrt{4x^2+1}}$$
b.	$$\frac{d}{dx} \left [ \tanh^{-1} (x^3) \right ]$$	$$=\frac{3x^2}{1-(x^3)^2}$$
		$$=\frac{3x^2}{1-x^6}$$

Example 5.8.7 Integration Using Inverse Hyperbolic Functions

a.	$$\int \frac{dx}{x\sqrt{4-9x^2}}$$	$$= int \frac{du}{ u \sqrt{a^2-u^2}}$$	Let \(a=2\) and \(u=3x\)
		$$=-\frac{1}{a} \ln \frac{a+\sqrt{a^2-u^2}}{\left | u \right |} +C$$
b.	$$ \int frac{dx}{5-4x^2}$$	$$= \frac{1}{2} \int \frac{du}{a^2-u^2}$$	Let \(a=\sqrt{5}\) and \(u=2x\).
		$$=\frac{1}{2} \left ( \frac{1}{2a} \ln \left | \frac{a+u}{a-u} \right | \right )+C$$
		$$=\frac{1}{4\sqrt{5}} \ln \left | \frac{\sqrt{5}+2x}{\sqrt{5}-2x} \right |+C$$	Back substitute

Internal Links

Parent Article: Calculus I 05 Logarithmic, Exponential, and Other Transcendental Functions