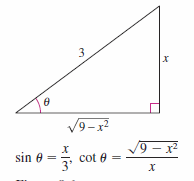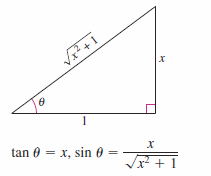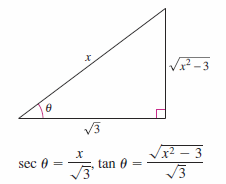Calculus II 08.04 Trigonometric Substitution
| Previous | Calculus II 08.03 Trigonometric Integrals |
| Next | Calculus II 08.05 Partial Fractions |
Contents
- 1 8.4 Trigonometric Substitution
- 1.1 Example 8.4.1 Trigonometric Substitution with \(u= a \sin \theta\)
- 1.2 Example 8.4.2 Trigonometric Substitution with \(u= a \tan \theta\)
- 1.3 Example 8.4.3 Trigonometric Substitution with Rational Powers
- 1.4 Example 8.4.4 Converting Integration Limits
- 1.5 Example 8.4.5 Choosing an Interval for \(\theta\)
- 1.6 Theorem 8.4.1 Special Integration Formulas where \((a > 0)\)
- 2 Internal Links
8.4 Trigonometric Substitution
- Use trigonometric substitution to solve an integral.
- Use integrals to model and solve real-life applications.
Trigonometric substitution is useful in solving radical integrals with the form
- \(\sqrt{a^{2}-u^{2}}\), \(\sqrt{a^{2}+u^{2}}\), and \(\sqrt{u^{2}-a^{2}}\)
by eliminating the radicals. The Pythagorean Trigonometric identities, listed below, are used to remove the radicals.
- $$ \cos^{2} \theta = 1 - \sin^{2} \theta $$
- $$ \sec^{2} \theta = 1 + \tan^{2} \theta $$
- $$ \tan^{2} \theta = \sec^{2} - 1 $$
For example, for \( a > 0\), let \(u=a \sin \theta \), where \(-\pi/2 \leqslant x \leqslant \pi /2\). This produces
| \(\sqrt{a^{2}-u^{2}}\) | \(= \sqrt{a^{2}-a^{2}\sin^{2} \theta}\) |
| \(= \sqrt{a^{2}(1-\sin^{2} \theta)}\) | |
| \(= \sqrt{a^{2}\cos^{2} \theta}= a \cos \theta\) |
Note that \(\cos x \geqslant 0\), because \(-\pi/2 \leqslant \theta \leqslant \pi /2\).
The restrictions on \(\theta\) ensures the function is one-to-one. These are the same intervals over which the arcsine, arctangent, and arcsecant are defined.
Example 8.4.1 Trigonometric Substitution with \(u= a \sin \theta\)
|
Find
Solution Note that no basic integration rule discussed so far applies. To apply trigonometric substitution note that
For the substitution let \(x=a \sin \theta = 3 \sin \theta \). Using differentiation and Figure 8.4.2 produces
Now trigonometric substitution can be applied.
|
Example 8.4.2 Trigonometric Substitution with \(u= a \tan \theta\)
|
Find
Solution Section 5.8 describes how inverse hyperbolic functions are used to evaluate integrals with the form
Inverse hyperbolic functions and trigonometric substitution can be combined to solve this problem. Let \(u=2x\), \(a=1\), and \(2x= \tan \theta\), as shown in Figure 8.4.3. This produces
Trigonometric substitution produces
|
Example 8.4.3 Trigonometric Substitution with Rational Powers
|
Trigonometric substitution can cover integrals involving expressions such as \((a^{2}-u^{2})^{n/2}\) by writing the expression as
Find
Solution Begin by writing \((x^{2}+1)^{3/2}\) as
Let \(a=1\) and \(u=x=\tan \theta\), as shown in Figure 8.4.4. Using
trigonometric substitution and be applied.
|
Example 8.4.4 Converting Integration Limits
|
Evaluate
Solution Section 4.5, Examples 4.5.8 and 4.5.9 describes how to determine integration limits for \(\theta\) that avoid converting back to \(x\). Because \( \sqrt{x^{2}-3} \)has the form \( \sqrt{x^{2}-a^{2}} \) consider a triangle where
as shown in Figure 8.4.5. This produces
To determine the upper and lower integration limits, use the substitution \( x=\sqrt{3} \sec \theta \)
|
Example 8.4.5 Choosing an Interval for \(\theta\)
Find
- $$ \int_{-2}^{-\sqrt{3}} \frac{ \sqrt{x^{2}-3} }{ x }\:dx $$
Solution When using trigonometric substitution to evaluate definite integrals make sure the values for \(\theta\) lie in ranges described in the first three guidelines described in this section. This definite integral is the same as in Example 8.4.4 except that the range is negative, \([-2, -\sqrt{3}]\). This makes \(u < -a\), which is covered in guideline 3. Choosing \(\theta\) such that \( \pi /2 < \theta \leqslant \pi\). The integral evaluates as follows
| $$ \int_{-2}^{-\sqrt{3}} \frac{ \sqrt{x^{2}-3} }{ x }\:dx $$ | $$= \int_{5 \pi /6}^{\pi} \frac{(-\sqrt{3}\tan \theta)(\sqrt{3}\sec \theta \tan \theta)d\theta}{\sqrt{3}\sec \theta}$$ |
| $$= \int_{5 \pi /6}^{\pi} -\sqrt{3}\tan^{2} \theta\: d\theta $$ | |
| $$= -\sqrt{3} \int_{0}^{\pi/6} (\sec^{2} \theta - 1)\: d\theta $$ | |
| $$= -\sqrt{3} \left[ \tan \theta - \theta \right]_{5 \pi /6}^{\pi} $$ | |
| $$= -\sqrt{3} \left[ (0-\pi) - \left( -\frac{1}{\sqrt{3}} - \frac{5\pi}{6} \right)\right] $$ | |
| $$= -1 + \frac{\sqrt{3}\pi}{6}\approx 0.0931 $$ |
Theorem 8.4.1 Special Integration Formulas where \((a > 0)\)
Trigonometric substitution can be used to complete the square. For instance, try finding the integral
- $$ \int \sqrt{x^{2}-2x}\:dx $$
Complete the square and write the integral as
- $$ \int \sqrt{(x-1)^{2}-1^{2}}\:dx $$
The integrand now has the form
- $$ \sqrt{u^{2}-a^{2}}$$
with \(u=x-1\) and \(a=1\). Trigonometric substitution can now be used to find the integral.
Theorem 8.4.1 describes these formulas.
| Theorem 8.4.1 Special Integration Formulas where \((a > 0)\) | |
|---|---|
| $$ \int \sqrt{a^{2}-u^{2}}\:du $$ | $$= \frac{1}{2} \left( a^{2} \arcsin \frac{u}{a} + u \sqrt{a^{2}-u^{2}} \right) + C $$ |
| $$ \int \sqrt{u^{2}-a^{2}}\:du $$ | $$= \frac{1}{2} \left( u \sqrt{u^{2}-a^{2}} - a^{2} \ln | u + \sqrt{u^{2}-a^{2}}| \right) + C, \: u > a $$ |
| $$ \int \sqrt{u^{2}+a^{2}}\:du $$ | $$= \frac{1}{2} \left( u \sqrt{u^{2}+a^{2}} + a^{2} \ln | u + \sqrt{u^{2}+a^{2}}| \right) + C $$ |
Example 8.4.6 Finding an Arc Length
|
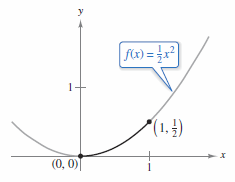
Find the arc length for the graph \(f(x)= \frac{1}{2} x^{2}\) from \(x=0\) to \(x=1\) as shown in Figure 8.4.6.
|
Example 8.4.7 Comparing two Fluid Forces
|
|
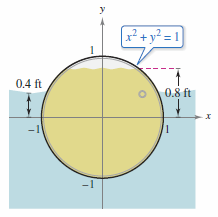
A sealed oil barrel of oil is floating in seawater as shown in Figures 8.4.7 and 8.4.8. The oil weighs 48 pounds per cubic foot. The seawater weighs 64 pounds per cubic foot. The barrel is lying on its side with the top 0.2 feet empty. Compare the fluid forces against one end from the inside and from the outside.
To find the fluid force pressing out from the inside, integrate between -1 and 0.8 where \(w=48\).
To find the fluid force pressing in from the outside, integrate between -1 and 0.4 where \(w=64\).
Integrate
then apply the variables. Let \(y= \sin u\), \(u= \arcsin y\), and \(\frac{dx}{du} = \cos u\).
The answer is
|
Internal Links
Parent Article: Calculus II 08 Integration Techniques