Calculus II 08.08 Improper Integrals

Previous	Calculus II 08.06 Integration by Tables and Other Integration Techniques
Next	Calculus II 09 Infinite Series

8.8 Improper Integrals[1]

• Evaluate an improper integral that has an infinite limit of integration.
• Evaluate an improper integral that has an infinite discontinuity.

Improper Integrals with Infinite Integration Limits

The unbounded region has an area equal to 1. Figure 8.8.1

The definition for a definite integral $$ \int_{a}^{b} f(x)\:dx $$ requires that the interval \([a,b]\) be finite and that \(f\) be continuous on \([a,b]\). This is called a proper integral. An improper integral has \( \infty \) as either or both limits or \(f\) has infinite discontinuities on the interval \([a,b]\). A function \(f\) has an infinite discontinuities at \(c\) from the right or left, $$ \lim_{x \to c} f(x) = \pm \infty . 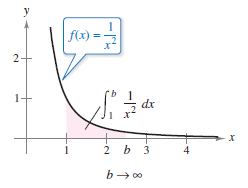$$ Consider the improper integral $$ \int_{1}^{b} \frac{dx}{x^{2}} = - \left. \frac{1}{x} \right ]_{1}^{b} = 1 - \frac{1}{b} $$ which is described graphically as the shaded region shown in Figure 8.8.1. Taking the limit as \(b \to \infty\) produces $$ \int_{1}^{\infty} \frac{dx}{x^{2}} = \lim_{b \to \infty} \left ( \int_{1}^{ b } \frac{dx}{x^{2}} \right ) = \lim_{b \to \infty} \left ( 1 - \frac{1}{b} \right ) = 1. $$ This improper integral can be interpreted as the area for the unbounded region between the graph for \(f(x)=1/x^{2}\) and the \(x\)-axis on the interval \([0,1]\).

Definition 8.8.1 Improper Integrals with Infinite Integration Limits

1. If \(f\) is continuous on the interval \([a, \infty)\), then

$$ \int_{a}^{ \infty } f(x)\:dx = \lim_{b \to \infty } \int_{a}^{b} f(x)\:dx . $$

2. If \(f\) is continuous on the interval \(( -\infty, b]\), then

$$ \int_{ - \infty }^{b} f(x)\:dx = \lim_{a \to -\infty } \int_{a}^{b} f(x)\:dx . $$

3. If \(f\) is continuous on the interval \(( -\infty, \infty) \), then

$$ \int_{ - \infty }^{ \infty} f(x)\:dx = \int_{-\infty }^{c} f(x)\:dx + \int_{c}^{ \infty } f(x)\:dx . $$

In the cases 1 and 2, the improper integral converges when the limit exists or it diverges otherwise. In case 3, the improper integral on the left diverges when either improper integral on the right diverges.

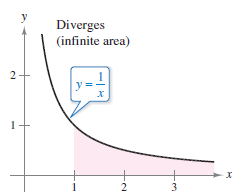
Example 8.8.1 An Improper Integral That Diverges

The unbounded region has an infinite area. Figure 8.8.2

Evaluate $$ \int_{1}^{ \infty } \frac{dx}{x}. $$ Solution $$ \int_{1}^{ \infty } \frac{dx}{x} $$ $$ = \lim_{b \to \infty} \int_{1}^{ b } \frac{dx}{x} $$ Take limit as \(b \to \infty \) $$ = \lim_{b \to \infty} \Bigg [ \ln x \Bigg ]_{1}^{ b } \:\:\:\: $$ Apply Log Rule $$ = \lim_{b \to \infty} ( \ln b - 0 ) $$ Apply Fundamental Theorem of Calculus $$ = \infty $$ Evaluate limit The limit does not exit. Therefore, the improper interval diverges as shown in Figure 8.8.1.

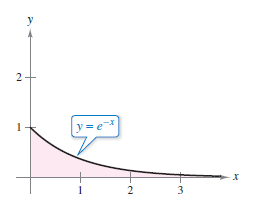
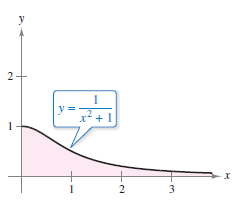
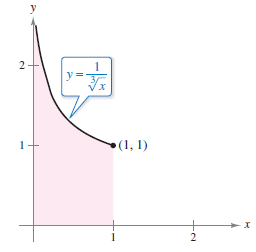
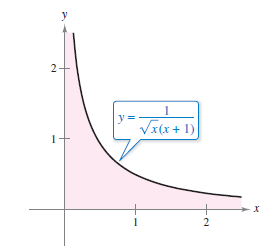
Example 8.8.2 Improper Integrals that Converge

The unbounded region has area equal to 1. Figure 8.8.3 The unbounded region has area equal to \(\pi/2\). Figure 8.8.4

Evaluate each improper integral. $$\text{a. } \int_{0}^{ \infty} e^{-x}\:dx $$ $$\text{b. } \int_{0}^{ \infty} \frac{1}{x^{2}+1} \:dx $$ Solution Apply the improper integrals definition to equations a and b. See Figure 8.8.3 and Figure 8.8.4 for a graphical solution. $$\text{ a. } \int_{0}^{ \infty} e^{-x}\:dx $$ $$ = \lim_{b \to \infty} \int_{0}^{ b} e^{-x}\:dx $$ $$\text{ b. } \int_{0}^{ \infty} \frac{1}{x^{2}+1} \:dx $$ $$ = \lim_{b \to \infty} \int_{0}^{ \infty} \frac{1}{x^{2}+1} \:dx$$ $$ = \lim_{b \to \infty} \Bigg [ -e^{-x} \Bigg ]_{0}^{ b}$$ $$ = \lim_{b \to \infty} \int_{0}^{ \infty} \Bigg[ \arctan x \Bigg]_{0}^{ b} $$ $$ = \lim_{b \to \infty} ( -e^{-b} +1)$$ $$ = \lim_{b \to \infty} \arctan b $$ $$ =1 $$ $$ = \frac{\pi}{2} $$

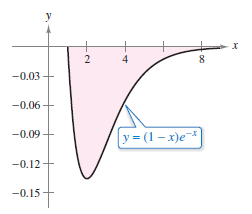
Example 8.8.3 Using L’Hôpital’s Rule with an Improper Integral

The unbounded region has area equal to \( |-1/e| \). Figure 8.8.5

Evaluate $$ \int_{1}^{ \infty} (1-x)e^{-x}\:dx $$ Solution Use integration by parts letting \(dv=e^{-x}\) and \(u=(1-x)\) to rewrite the equation so that the Improper Integral definition can be applied. $$ \int (1-x)e^{-x}\:dx $$ $$ = -e^{-x}(1-x) - \int e^{-x}\:dx $$ $$ = -e^{-x} + xe^{-x} + e^{-x} + C$$ $$ = xe^{-x} + C$$ The improper integral definition can be applied. $$ \int_{1}^{ \infty} (1-x)e^{-x}\:dx $$ $$ = \lim_{b \to \infty} \Bigg [ xe^{-x} \Bigg ]_{1}^{ b}$$ $$ = \lim_{b \to \infty} \left ( \frac{b}{e^{b}}- \frac{1}{e} \right) $$ $$ = \lim_{b \to \infty} \frac{b}{e^{b}}- \lim_{b \to \infty} \frac{1}{e} $$ Use L’Hôpital’s Rule to find the first limit. $$ \lim_{b \to \infty} \frac{b}{e^{b}} = \lim_{b \to \infty} \frac{1}{e^{b}}=0 $$ Using back substitution produces \( - 1/e\) as shown in Figure 8.8.5. $$ \int_{1}^{ \infty} (1-x)e^{-x}\:dx $$ $$ = \lim_{b \to \infty} \frac{b}{e^{b}} - \lim_{b \to \infty} \frac{1}{e}$$ $$ = 0 - \frac{1}{e} = - \frac{1}{e} $$

Example 8.8.4 Infinite Upper and Lower Limits of Integration

The unbounded region has area equal to \( \pi / 2 \). Figure 8.8.6

Evaluate $$ \int_{- \infty}^{ \infty} \frac{e^{-x}}{1+e^{2x}}\:dx $$ Solution The integrand is continuous on \( (- \infty, \infty ) \). Split the integrand in two using \(c=0\) as shown in Figure 8.8.6. $$ \int_{- \infty}^{ \infty} \frac{e^{-x}}{1+e^{2x}}\:dx $$ $$\int_{- \infty}^{0} \frac{e^{-x}}{1+e^{2x}}\:dx + \int_{0}^{ \infty} \frac{e^{-x}}{1+e^{2x}}\:dx$$ $$ = \lim_{ b \to -\infty } \Bigg[ \arctan e^{x} \Bigg]_{b}^{0} + \lim_{ b \to \infty } \Bigg[ \arctan e^{x} \Bigg]_{0}^{b}$$ $$ = \lim_{ b \to -\infty } \Bigg( \frac{\pi}{4} - \arctan e^{b} \Bigg) + \lim_{ b \to \infty } \Bigg( \arctan e^{b} -\frac{\pi}{4} \Bigg)$$ $$ = \frac{\pi}{4} - 0 + \frac{\pi}{2} - \frac{\pi}{4}= \frac{\pi}{2}$$

Example 8.8.5 Sending a Spacecraft into Orbit

The work required to move a 15-metric-ton space Spacecraft an unlimited distance away from Earth is about \(6.984 \cdot 10^{11}\) foot-pounds. Figure 8.8.7

Example 7.5.3 demonstrated that 10,000 mile-tons of work is required to propel a 15-metric-ton Spacecraft to an 800 mile altitude. How much work is required to propel the same spacecraft an to an unlimited altitude? Solution Use the integral in Example 7.5.3 and replace 4800 miles as the upper bound with \( \infty \) and write. $$ W $$ $$ = \int_{4000}^{ \infty } \frac{240,000,000}{x^{2}} \:dx$$ $$ = \lim_{ b \to \infty } \left[ -\frac{240,000,000}{x^{2}} \right]_{4000}^{ b }$$ $$ = \lim_{ b \to \infty } \left( -\frac{240,000,000}{b} + \frac{240,000,000}{4000} \right) $$ $$ = 60,000 mile-tons $$ $$ \approx 60,000 \cdot 10^{11} foot-pounds. $$ In SI units where 1 foot-pound \(\approx \) 1.35582 joules the work done is \( W \approx 9.469 \cdot 10^{11} \) joules.

Improper Integrals with Infinite Discontinuities

Some integrals have an infinite discontinuity at or between the integration limits.

Definition 8.8.2 Improper Integrals with Infinite Discontinuities

1. If \(f\) is continuous on the interval \([a, b )\) and has an infinite discontinuity at \(b\), then

$$ \int_{a}^{ b } f(x)\:dx = \lim_{c \to b^{-} } \int_{a}^{c} f(x)\:dx . $$

2. If \(f\) is continuous on the interval \(( a, b]\) and has an infinite discontinuity at \(a\), then

$$ \int_{ a }^{b} f(x)\:dx = \lim_{c \to a^{-} } \int_{c}^{b} f(x)\:dx . $$

3. If \(f\) is continuous on the interval \([ a, b ] \), except for some \(c\) in \(( a, b ) \) at which \(f\) has an infinite discontinuity, then

$$ \int_{ a }^{ b } f(x)\:dx = \int_{ a }^{c} f(x)\:dx + \int_{c}^{ b } f(x)\:dx . $$

In the cases 1 and 2, the improper integral converges when the limit exists or it diverges otherwise. In case 3, the improper integral on the left diverges when either improper integral on the right diverges.

Example 8.8.6 An Improper Integral with an Infinite Discontinuity

Infinite discontinuity at \(x=0\). Figure 8.8.8

Evaluate $$ \int_{ 0 }^{ 1 } \frac{1}{\sqrt[3]{x}} \:dx. $$ Solution The integrand has an infinite discontinuity at \(x=0\), as shown in Figure 8.8.8. The integrand can be rewritten and solved as below. $$ \int_{ 0 }^{ 1 } x^{-1/3} \:dx $$ $$ = \lim_{b \to 0^{+}} \left[ \frac{x^{2/3}}{2/3} \right]_{b}^{1}$$ $$ = \lim_{b \to 0^{+}} \frac{3}{2} (1-b^{2/3}) = \frac{3}{2}$$

Example 8.8.7 An Improper Integral That Diverges

Evaluate

$$ \int_{ 0 }^{ 2 } \frac{1}{ x^{3}} \:dx. $$

Solution The integrand has an infinite discontinuity at \(x=0\). The integrand can be rewritten and solved as below.

$$ \int_{ 0 }^{ 2 } \frac{1}{ x^{3}} \:dx $$	$$ = \lim_{b \to 0^{+}} \left[ -\frac{1}{2x^{2}} \right]_{b}^{2}$$
	$$ = \lim_{b \to 0^{+}} \left( -\frac{1}{8} + \frac{1}{2b^{2}} \right)$$
	$$ = \infty $$

The improper integral diverges as x approaches 0.

Example 8.8.8 An Improper Integral with an Interior Discontinuity

Infinite discontinuity at \(x=0\). Figure 8.8.9

Evaluate $$ \int_{ -1 }^{ 2 } \frac{1}{ x^{3}} \:dx. $$ Solution The integrand has an infinite discontinuity at the interior point, between the limits, \(x=0\), as shown in Figure 8.8.9. Split the integrand where \(x=0\) and integrate as in Example 8.8.7. $$ \int_{ -1 }^{ 2 } \frac{1}{ x^{3}} \:dx = \int_{ -1 }^{ 0 } \frac{1}{ x^{3}} \:dx + \int_{ 0 }^{ 2 } \frac{1}{ x^{3}} \:dx $$ Note from Example 8.8.7 that the second integral diverges. Therefore, the original improper integral also diverges.

Example 8.8.9 A Double Improper Integral

The unbounded region has the area \(\pi\). Figure 8.8.10

Evaluate $$ \int_{ 0 }^{ \infty } \frac{1}{ \sqrt{x}(x+1)} \:dx $$ as shown in Figure 8.8.10. Solution Split the integral at a convenient point, \(x=1\), and write $$ \int_{ 0 }^{ \infty } \frac{1}{ \sqrt{x}(x+1)} \:dx $$ $$ = \int_{ 0 }^{ 1 } \frac{1}{ \sqrt{x}(x+1)} \:dx + \int_{ 1 }^{ \infty } \frac{1}{ \sqrt{x}(x+1)} \:dx $$ $$ = \lim_{b \to 0^{+}} \Bigg [ 2 \arctan \sqrt{ x } \Bigg ]_{ b }^{ 1 } + \lim_{ c \to \infty } \Bigg [ 2 \arctan \sqrt{ x } \Bigg ]_{ c }^{ 1 }$$ $$ = \lim_{b \to 0^{+}} ( 2 \arctan 1 - 2 \arctan \sqrt{ b }) + \lim_{ c \to \infty } ( 2 \arctan \sqrt{ c } - 2 \arctan 1 )$$ $$ = 2 \left ( \frac{\pi}{4} \right ) - 0 + 2 \left ( \frac{\pi}{2} \right ) - 2 \left ( \frac{\pi}{4} \right ) $$ $$ = \pi $$ Line two in the solution shows the double discontinuity clearly. The lower limit, \(x=0\), has an infinite discontinuity. The upper limit, \( \infty \), has an infinite integration.

Example 8.8.10 An Application Involving Arc Length

The circle's circumference is \(2\pi\). Figure 8.8.11

Use the formula for arc length to show that a circle with radius 1 has the circumference \(2 \pi\) as shown in Figure 8.8.11. Solution Recall the formula for a circle with radius 1 is \(x^{2}+y^{2} = 1\). To simplify, consider a quarter circle by solving for \(y\), \(y = \sqrt{1-x^{2}} \) over the range \( 0 \leqslant x \leqslant 1 \) as shown in Figure 8.8.11. Therefore, the arc length for the quarter circle is given by the improper integral $$ S $$ $$ = \int_{ 0 }^{ 1 } \sqrt{1+(y')^{2}} \:dx $$ $$ = \int_{ 0 }^{ 1 } \sqrt{1+ \left ( \frac{-x}{\sqrt{1-x^{2}}} \right )^{2}} \:dx $$ $$ = \int_{ 0 }^{ 1 } \frac{1}{\sqrt{1-x^{2}}} \:dx $$ This integral is improper because it has an infinite discontinuity at \(x=1\). Solving produces $$ S $$ $$ = \int_{ 0 }^{ 1 } \frac{1}{\sqrt{1-x^{2}}} \:dx $$ $$ = \lim_{ b \to 1^{ - }} \bigg [ \arcsin x \bigg ]_{ 0 }^{ b } $$ $$ = \lim_{ b \to 1^{ - }} (\arcsin b - \arcsin 0 ) $$ $$ = \frac{\pi}{2}-0 $$ $$ = \frac{\pi}{2}. $$ Multiply by 4 to restore the entire circle and the circumference is \(4S = 2\pi\).

Theorem 8.8.1 Improper Integral that is Bounded and Unbounded

$$ \int_{ 1 }^{ \infty } \frac{1}{x^{p}} \:dx = = \left\{\begin{matrix} \frac{1}{p-1}, & p >1 \\ diverges, & p \leqslant 1 \end{matrix}\right. $$

Example 8.8.11 An Application Involving a Rotated Solid

The solid formed by rotating \(f(x)=1/x\) about the \(x\)-axis where \(( 1 \leqslant x ) \) is called Gabriel's Horn[2] as shown in Figure 8.8.12. Show that this solid has a finite volume and an infinite surface area.
Solution Use the Disk Method and Theorem 8.8.1 to determine the volume

$$ V $$	$$ = \pi \int_{ 1 }^{ \infty } \left ( \frac{1}{x} \right )^{2} \:dx \:\:\:\: $$	Theorem 8.8.1, \(p = 2 > 1\)
	$$ = \pi \left ( \frac{1}{2-1} \right ) $$
	$$ = \pi. $$

The surface area is determined by

$$ S = 2 \pi \int_{ 1 }^{ \infty }f(x) \sqrt{1+[f'(x)]^{2}} \:dx = 2 \pi \int_{ 1 }^{ \infty } \frac{1}{x} \sqrt{1+ \frac{1}{x^{4}}} \:dx. $$

Because

$$ 1 < \sqrt{1+ \frac{1}{x^{4}}} $$

on the interval \([1, \infty) \), and the improper integral

$$ \int_{ 1 }^{ \infty } \frac{1}{x} \:dx $$

diverges, the improper integral

$$ \int_{ 1 }^{ \infty } \frac{1}{x} \sqrt{1+ \frac{1}{x^{4}}} \:dx $$

also diverges. Therefore, the surface area is infinite.

Gabriel's Horn as a finite volume and infinite surface area.
Figure 8.8.12

Internal Links

Parent Article: Calculus II 08 Integration Techniques