Calculus I 03.06 Curve Sketching

Previous	Calculus I 03.05 Limits at Infinity
Next	Calculus I 03.07 Optimization Problems

3.6 Curve Sketching Summary

• Analyze and sketch a function's graph.

Analyzing a Function's Graph

Figure 3.6.1

When sketching the graph for a function normally only a view is shown, not the entire graph. Which view to sketch crucial. For example, which view shown in Figure 3.6.1 better represents the graph for \(f(x)=x^3-25x^2+75x-20?\) The second view shows more interesting features. The \(x\)-intercept and a horizontal tangent line. But would a third view reveal other interesting features? To answer this use calculus to interpret the first and second derivatives. Below are guidelines for determining a good view for a graph. Guidelines for Analyzing Function Graphs Determine the following for the function.     1. Domain     2. Range     3. Intercepts     4. Asymptotes     5. Graph's Symmetry     6. \({f}'(x)\) and it's \(x\)-values.     7. \({f}''(x)\) and it's \(x\)-values. Always take the first and second derivatives for the function and solve for the zeros. Note how important algebra is in solving the equations. \(f(x)=0,\:\:\:\:{f}'(x),\:\:\:\: \text{ and }{f}''(x).\)

Example 3.6.1 Sketching the Graph for a Rational Function

Applying calculus determines all the graph's characteristics. Figure 3.6.2

Analyze and sketch the graph for $$f(x)=\frac{2(x^2-9)}{x^2-4}.$$ Solution Table 3.6.1 shows how the test intervals are used to determine the graph's characteristics, as shown in Figure 3.6.2. Table 3.6.1 \(f(x)\) \({f}'(x)\) \({f}''(x)\) Graph Characteristic \(-\infty < x < -2\) - - Decreasing, concave downward \( x=-2\) Undef. Undef. Undef. Vertical asymptote \( -2 < x < 0 \) - + Decreasing, concave upward \( x=0\) \(\frac{9}{2}\) 0 + Relative minimum \( 0<x<2 \) + + Increasing, concave upward \(x=2\) Undef. Undef. Undef. Vertical asymptote \( 2< x< \infty\) + - Increasing, concave downward Creating a table like Table 3.6.1, ensures all the characteristics and none are unaccounted for.

Example 3.6.2 Sketching the Graph for a Rational Function

Figure 3.6.3

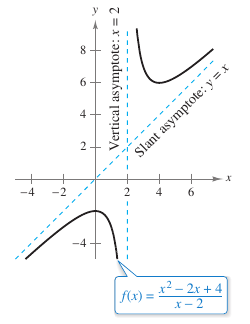
Analyze and sketch the graph for $$f(x)=\frac{x^2-2x+4}{x-2}.$$ Solution Table 3.6.2 shows how the test intervals are used to determine the graph's characteristics, as shown in Figure 3.6.3. Table 3.6.2 \(f(x)\) \({f}'(x)\) \({f}''(x)\) Graph Characteristic \(-\infty < x < 0\) + - Increasing, concave downward \( x=0\) -2 0 - Relative Maximum \( 0 < x < 2 \) - - Decreasing, concave downward \( x=2\) Undef. Undef. Undef. Vertical asymptote \( 2<x<24 \) - + Decreasing, concave upward \(x=4\) 6 0 + Decreasing, concave upward \(4< x< \infty\) + + Increasing, concave upward

Figure 3.6.4

$$f(x)=$$ $$\frac{x^2-2x+4}{x-2}$$     Write original equation $$=x+\frac{4}{x-2}$$     Rewrite using long division Note the graph for \(f\) approaches the slant asymptote \(y=x\) as \(x\) approaches \(-\infty\) or \(\infty\).

Example 3.6.3 Sketching the Graph for a Radical Function

Figure 3.6.5

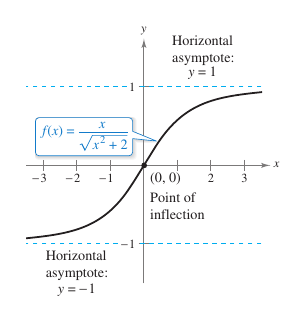
Analyze and sketch the graph for $$f(x)=\frac{x}{\sqrt{x^2+2}}.$$ Solution $${f}'(x)=\frac{2}{(x^2+2)^{3/2}}$$     Find first derivative. $${f}''(x)=\frac{6x}{(x^2+2)^{5/2}}$$     Find second derivative. The graph has only one intercept, \((0,0)\). It has no vertical asymptotes, but it has two horizontal asymptotes: \(y=1\), to the right, and \(y=-1\), to the left. The function has no critical numbers and one possible inflection point at \(x=0\). The function domain is all real numbers, and the graph is symmetric with respect to the origin. The analysis is shown in Table 3.6.3, and shown in Figure 3.6.3. Table 3.6.3 \(f(x)\) \({f}'(x)\) \({f}''(x)\) Graph Characteristic \(-\infty < x < 0\) + + Increasing, concave upward \( x=0\) 0 \(\frac{1}{\sqrt{2}}\) 0 Inflection point \( 0 < x < \infty \) + - Increasing, concave downward

Example 3.6.4 Sketching the Graph for a Radical Function

Figure 3.6.6

Analyze and sketch the graph for $$f(x)=2x^{5/3}-5x^{4/3}.$$ Solution $${f}'(x)=\frac{10}{3}x^{1/3}(x^{1/3}-2)$$     Find first derivative. $${f}''(x)=\frac{20(x^{1/3}-1)}{9x^{2/3}}$$     Find second derivative. The function has two intercepts, \((0,0)\) and \((\frac{125}{8},0)\). There are no horizontal or vertical asymptotes. The function has two critical numbers \(x=0\) and \(x=8\) and two possible inflection points at \(x=0\) and \(x=1\). The domain is all real numbers. The analysis is shown in Table 3.6.4, and shown in Figure 3.6.4. Table 3.6.4 \(f(x)\) \({f}'(x)\) \({f}''(x)\) Graph Characteristic \(-\infty < x < 0\) + - Increasing, concave downward \( x=0\) 0 0 Undef Relative maximum \( 0 < x < 1 \) - - Decreasing, concave downward \( x=1 \) -3 - 0 Inflection point \( 1 < x < 8 \) - + Decreasing, concave upward \( x=8 \) -16 0 + Relative minimum \( 0 < x < \infty \) + + Increasing, concave upward

Example 3.6.5 Sketching the Graph for a Polynomial Function

A polynomial function with even degree must have at least one relative extremum Figure 3.6.7

Analyze and sketch the graph for \(f(x)=x^4-12x^3+48x^2-64x.\) Solution Begin by factoring to obtain \(f(x)\) \(=x^4-12x^3+48x^2-64x\) \(=x(x-4)^3.\) Using the factored form for \(f(x)\) produces the following analysis. The analysis is shown in Table 3.6.5, and shown in Figure 3.6.7. Table 3.6.5 \(f(x)\) \({f}'(x)\) \({f}''(x)\) Graph Characteristic \(-\infty < x < 1\) - + Decreasing, concave upward \( x=1\) -27 0 + Relative minimum \( 1 < x < 2 \) + + Increasing, concave upward \( x=2 \) -16 + 0 Inflection point \( 2 < x < 4 \) + - Increasing, concave downward \( x=4 \) 0 0 0 Inflection point \( 4 < x < \infty \) + + Increasing, concave upward

The fourth-degree polynomial function in Example 3.6.5 has one relative minimum and no relative maxima. In general, a polynomial function with degree \(n\) can have at most \(n-1\) relative extrema, and at most \(n-2\) inflection points. Polynomial functions with even degree must have at least one relative extremum.

The “end behavior” for a polynomial function graph is determined by its leading coefficient and its degree. For example, because the polynomial in Example 3.6.5 has a positive leading coefficient, the graph rises to the right. Because the degree is even the graph also rises to the left.

Example 3.6.6 Sketching the Graph for a Trigonometric Function

Figure 3.6.8

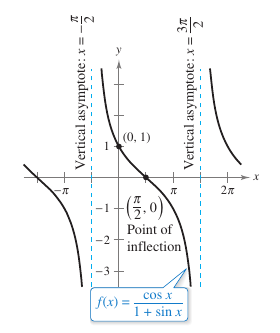
Analyze and sketch the graph for $$f(x)=\frac{\cos x}{1+\sin x}.$$ Solution Because the function has a \(2\pi\) period restrict the analysis to any interval with length \(2\pi\). Here \((-\pi/2,3\pi/2)\) was chosen. The analysis is shown in Table 3.6.6, and shown in Figure 3.6.8. Table 3.6.6 \(f(x)\) \({f}'(x)\) \({f}''(x)\) Graph Characteristic $$x=-\frac{\pi}{2}$$ Undef. Undef. Undef. Vertical asymptote $$-\frac{\pi}{2},x< \frac{\pi}{2}$$ - + Decreasing, concave upward $$x=\frac{\pi}{2}$$ 0 -\(\frac{1}{2}\) 0 Inflection point $$\frac{\pi}{2}<x< \frac{3\pi}{2}$$ - - Decreasing, concave downward $$x=\frac{3\pi}{2}$$ Undef. Undef. Undef. Vertical asymptote By substituting \(-\pi/2\) or \(3\pi/2\) into function produces the form \(0/0\). This is called an indeterminate form which is described in Section 8.7. To determine that the function has vertical asymptotes at these two values, rewrite \(f\) as $$f(x)=\frac{\cos x}{1+\sin x}=\frac{(\cos x)(1-\sin x)}{(1+\sin x)(1-\sin x)}=\frac{(\cos x)(1-\sin x)}{\cos^2 x}=\frac{1-\sin x}{\cos x}.$$ In this form it is clear the graph for \(f\) has two vertical asymptotes at \(x=-\pi/2\) and \(x=3\pi/2\).

Internal Links

Parent Article: Calculus I 03 Differentiation Applications