Calculus I 03.07 Optimization Problems

Previous	Calculus I 03.06 Curve Sketching
Next	Calculus I 03.08 Newton’s Method

3.7 Optimization Problems

• Solve applied maximum and minimum problems.

Applied Maximum and Minimum Problems

A common application for calculus is determining maximum and minimum values. Superlatives such as greatest profit, least cost, least time, greatest voltage, optimum size, least size, greatest strength, and greatest distance all require determining maximum and minimum values. Consider Example 3.7.1.

Example 3.7.1 Finding Maximum Volume

Open box with square base: \(S=x^2+4xh=108\) Figure 3.7.1

A manufacturer wants to design an open box having a square base and a 108 square inches in surface area, as shown in Figure 3.7.1. What dimensions will produce a box with maximum volume? Solution Because the box has a square base, its volume is \(V=x^2h.\)     Primary equation This equation is called the primary equation because it provides the formula for the quantity for optimization. The surface area for the box is \(S\) \(=(\text{base area})+(\text{area for four sides})\)       \(108\) \(=x^2+4h.\)    Secondary equation Because the goal is maximizing \(V\) write it as a function with one variable. To accomplish this solve the secondary equation for \(h\) and substitute that into the primary equation. Solve the secondary equation. \(x^2+4xh\) \(=108\)     Flip the equation \(4xh\) \(=108-x^2\) \(h\) $$=\frac{108-x^2}{4x}$$ Substitute it into the primary equation. \(V\) \(=x^2h\)     Function with two variables. $$=x \left ( \color{red}{ \frac{108-x^2}{4x}} \right )$$     Substitute for \(h\) $$=27x-\frac{x^3}{4}.$$     Function with one variables. Before finding which \(x\)-value will maximize \(V\) determine the feasible domain. As in, what values for \(x\) make sense in this problem? The volume is \(V \leq 0\). Any value for \(x\) must be non-negative. The area for the base is \(A=x^2\) and is at most 108. This makes the feasible domain \(0 \leq x \leq \sqrt{108}.\) To maximize \(V\), find the critical numbers for the volume function on the interval \((0,\sqrt{108})\). $$\frac{dV}{dx}$$ $$=27-\frac{3x^2}{4}$$     Differentiate with respect to \(x\). $$27-\frac{3x^2}{4}$$ \(=0\)     Set derivative equal to 0. \(3x^2\) \(=108\)     Simplify \(x\) \(=\pm 6\)     Critical numbers The critical numbers are \(x= \pm 6\). Reject \(x=-6\) because it is outside the domain. Evaluating \(V\) at the critical number \(x=6\) and at the endpoints the domain produces \(V(0)=0,\:V(6)=108, \text{ and }V(108)=0\) produces a maximum when \(x=6\). The dimensions for the box are 6x6x3 inches.

Example 3.7.1 demonstrated there are infinitely many open boxes having 108 square inches in surface area. What shaped box might yield a maximum volume? Should the box be tall, squat, or nearly cubical? One method is calculating a few volumes and shapes, as shown in Figure 3.7.2.Remember that solving a problem starts with understanding what the problem is in detail.

Which box has the largest volume?
Figure 3.7.2

Example 3.7.1 illustrates the following guidelines for solving applied maximum and minimum problems.

Guidelines for Solving Applied Maximum and Minimum Problems

1. Identify all given quantities and all quantities to be determined. If possible, make a sketch.
2. Write a primary equation for the quantity to maximize or minimize.
3. Reduce the primary equation to one with a single independent variable. This may using secondary equations relating the independent variables in the primary equation.
4. Determine the feasible domain for the primary equation.
5. Determine the desired maximum or minimum values using the techniques discussed in Sections 3.1 through 3.4 by finding the critical numbers and comparing them with the interval endpoints.

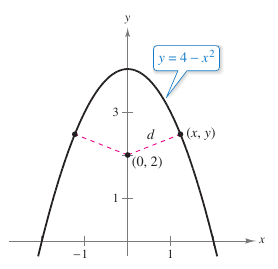
Example 3.7.2 Finding Minimum Distance

Figure 3.7.3

Which points on the graph for \(y=4-x^2\) are closest to the point \((0,2)\). Solution Figure 3.7.3 shows there are two points at a minimum distance from the point \((0,2)\). The distance between that and a point \((x,y)\) on the graph is \(d=\sqrt{(x-0)^2+(y-2)^2}.\)     Primary equation Using the secondary equation \(y=4-x^2\) the primary equation can be rewriten as \(d\) \(=\sqrt{x^2+(\color{red}{4-x^2}-2)^2}\) \(=\sqrt{x^4-3x^2+4}.\) The variable \(d\) is smallest when the expression inside the radical is smallest. Find the critical numbers for \(f(x)=x^4-3x^2+4.\) Note the domain for \(f\) is the entire real number line, therefore there are no endpoints to consider. The derivative for \(f\) \({f}'(x)\) \(=4x^3-6x\) \(=2x(2x^2-3)\) is zero when $$x=0,\:\sqrt{ \frac{3}{2}}, \: -\sqrt{ \frac{3}{2}}.$$ Using the First Derivative Test verifies that \(x=0\) yields a relative maximum. But \(x=\sqrt{3/2}\) and \(x=-\sqrt{3/2}\) yield a minimum distance. Therefore, the closest points are \((\sqrt{3/2},5/2)\) and \((-\sqrt{3/2},5/2)\).

Example 3.7.3 Finding Minimum Area

Minimize the area. Figure 3.7.4

Place 24 printable square inches on a rectangular page. The top and bottom margins are \(1\frac{1}{2}\) inches. The left and right margins are 1 inch, as shown in Figure 3.7.4. Minimize the page area, \(A\), to minimize the paper used. Solution Let \(A\) be the area. \(A=(x+3)(y+2)\)     Primary equation The printable area inside the margins is \(24=xy\)     Secondary equation Solving the secondary equation for \(y\) produces $$y=\frac{24}{3}.$$ Substitution into the primary equation produces $$A=(x+3) \left ( \color{red}{ \frac{24}{x}}+2 \right )=30+2x+\frac{72}{x}.$$     Function with one variable Because \(x\) must be positive only the values for \(A\) where \(x>0\) are viable. Differentiate with respect to \(x\) to find the critical numbers, $$\frac{dA}{dx}=2-\frac{72}{x^2}$$ and note the derivative is zero when \(x^2=36\), or \(x= \pm 6\). Therefore, the critical numbers are \(x= \pm 6\). Discard \(x=-6\) because it is outside the domain. The First Derivative Test confirms that \(A\) is a minimum when \(x=6\). Finally, \(y=\frac{24}{6}=4\) and the page should be \(x+3=9\) inches by \(y+2=6\) inches.

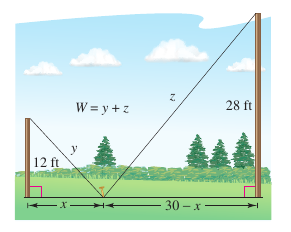
Example 3.7.4 Finding Minimum Length

The variable \(x\) varies between 0 and 30. Figure 3.7.5

Two posts, one 12 feet high and the other 28 feet high, stand 30 feet apart. A wire stays each running from the top to the ground and are both attached to a single stake. Where should the stake be placed for the shortest wire? Solution Let \(W\) be the wire length we are minimizing. The primary equation can be written as \(W=y+z.\)    Primary equation Rather than solving for \(y\) in \(z\) terms, or the reverse, solve for both \(y\) and \(z\) in \(x\) terms, a third variable, as shown in Figure 3.7.5. Applying the Pythagorean Theorem produces \(y^2\) \(=x^2+12^2\) \(z^2\) \(=(30-x)^2+28^2\) which implies that \(y\) \(=\sqrt{x^2+144}\) \(z\) \(=\sqrt{x^2-60x+1684}.\) Rewrite the primary equation as \(W\) \(=y+z\) \(=\sqrt{x^2+144} + \sqrt{x^2-60x+1684}, \: 0 \leq x \leq 30.\) Differentiating \(W\) with respect to \(x\) yields $$\frac{dW}{dx}=\frac{x}{\sqrt{x^2+144}}+\frac{x-30}{\sqrt{x^2-60x+1684}}.$$ By letting $$\frac{dW}{dx}=0$$ yields Because \(x=-22.5\) is not in the domain and \(W(0) \approx 53.04, \: W(9)=50, \text{ and }W(30)\approx60.31\) the conclusion is the wire should be staked at 9 feet from the 12-foot pole.

In the first four examples, the extreme value occurred at a critical number. This happens often, but remember that an extreme value can also occur at an interval endpoint, as shown in Example 3.7.5.

Example 3.7.5 Finding Minimum Length

The variable \(x\) varies between 0 and 30. Figure 3.7.6

A wire four feet long is formed into a square and a circle. How much wire should be used to enclose the maximum total area? Solution Figure 3.7.6 illustrates the total area. The primary equation is \(A\) \(=(\text{square area})+(\text{circle area})\) \(A\) \(=x^2+\pi r^2.\)     Primary equation Because the wire is 4 feet long, the total perimeter is \(4\) \(=(\text{ square's perimeter})+(\text{circle's area})\) \(4\) \(=4x+2\pi r.\) Therefore, $$r=\frac{2(1-x)}{\pi},$$ by substituting this into the primary equation produces $$A$$ $$=x^2+\pi \left [ \color{red}{\frac{2(1-x)}{\pi}} \right ]^2$$ $$=x^2+ \frac{4(1-x)^2}{\pi}$$ $$=\frac{1}{\pi}[(\pi +4)x^2-8x+4].$$ The feasible domain is \(0 \leq x \leq 1\), as restricted by the square's perimeter. Because $$\frac{dA}{dx}=\frac{2(\pi+4)x-8}{\pi}$$ the only critical number in \((0,1)\) is $$x=\frac{4}{(\pi+4)}\approx 0.56.$$ Using \(A(0) \approx 1.273, \: A(0.56) \approx 0.56, \text{ and } A(1)=1\) the conclusion is the maximum are occurs when \(x=0\). That is, all the wire is used for the circle.

Internal Links

Parent Article: Calculus I 03 Differentiation Applications